img200

200

Podstawowymi wielkościami S3i długość o, tseee kg, czas a, temperatura K. Ilość podstawowych wielkości wynosi z ■ 4* Wybierane spośród parametrów funkcji 4 wielkości różr.ięce się pomiędzy sobę wymia-rŁja- i zawierajfcci- T.ezyetKit i wyciory pocstfc*owe_f tworzy się odpowiednie iloczyny potęgowe. Ilość wykładników potęgowych równe jest Ilości wybranych wielkości. Wartości 4 wykładników nośna obliczyć tylko z układu \ rćrssń pod rerunkien, dc'układ ten nic będzie zewieml równać ióen-tycznych. Identyczność równać świadczy o zależności wymiarowsj^pomięćzy przyjętymi wielkościami. ¥ omawianym przykładzie wymiarowo zależnymi bo: długość 1, prędkość w oraz lepkość V , gdyt wymiar lepkości jest iloczynem wymiarów długości i prędkości. W układzie 4 równać otrzymuje się wówczas 2 równanie identyczne, a zatem można obliczyć wartości tylko 3 wykładników potęgowych 1 dlatego ilość wybranych wielkości należy ograniczyć do 3* W takin przypadku ilość iloczynów E będzie równa .6-3*3. Przyjmując l,Jl,V, otrzymujemy naatępujęoe równania:

h

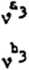
Równanie wymiarowe dla K₁ będzie

Łj - kg $r2    Z'' b ¹ kg ² m

kg 0 • 1 ♦ ®2 m 0 • •₁ ♦ o₂ + źa^

*    0--3-3e₂**3

K 0 » - 1 -

2

T»2

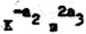
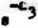
Z rozwiązania otrzymujemy

«₁ - 1j a₂ » -1|    • 0

Łj • ^ * ■ Su liczbę Suaaelta Równanie wymiarowe dla Eg

^    . .-¹ .^Łl k^² ^ .‘^3bi

kg O • h₂

a O * 1 ♦    ♦ b₂ ♦ 2bj

-b₀    2b, -

3.^3