img310

M

M

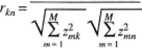
(15.23)

Licznik tego wzoru jest iloczynem skalarnym dwóch wektorów zmiennych Z_k i Z„:

M

£^^ = £ll£lcosa    (15.24)

a mianownik jest iloczynem długości tych samych wektorów. Wzór (23) przyjmie zatem postać:

(15.25)

IZ* I IZ„ I cos a

r_kn =-— =cosct

IZ*IIZJ

Zgodnie z warunkiem (15.22) współczynniki korelacji różnych zmiennych, tzn. elementy spoza głównej przekątnej macierzy R i R ’są sobie równe, tzn.:

(15.26)

^rkn = ^rkn =COStt

Elementy znajdujące się na głównej przekątnej macierzy R są interpretowane jako długości zmiennych-wektorów. Elementy na głównej przekątnej macierzy * są zasobami zmienności wspólnej, a więc obejmują tylko pewną część „długości” wektorów-zmicnnych Z*

IZJ =    < 1

Zatem macierze R i R ' zawierają wszystkie podstawowe informacje o zmiennych. Elementy spoza głównej przekątnej określają kąty między wektorami, a elementy z głównej przekątnej określają długości wektorów. Macierze R i R' wyznaczają w jednoznaczny sposób całą konfigurację wektorów. Również pozostałe wielkości występujące w analizie czynnikowej możemy zinterpretować geometrycznie. Na podstawie warunku (15.7) interpretujemy czynniki Fj — są one wektorami o jednostkowej długości, a kąty między nimi mają 90*. Czynniki są więc interpretowane jako osie prostokątnego układu współrzędnych.

Ładunki czynnikowe interpretuje się natomiast jako rzuty wektorów-zmiennych na osic-czynniki. Zależność (15.15) wyjaśnia, że ładunek czynnikowy m-tego czynnika i /i-tej zmiennej jest współczynnikiem korelacji między /i-tą zmienną i m-tym czynnikiem jako cosinus kąta zawartego między tymi wielkościami. A zatem

310