img314

Opisanemu przekształceniu geometrycznie odpowiada obrót kierunków głównych określających składowe główne. Obrót taki pozwala łatwiej zinterpretować otrzymane wyniki. Normalnie wszystkie ładunki mają wartości z przedziału (-1, 1) i na ich podstawie trudno jest określić najważniejsze czynniki. Po dokonaniu ortogonalnej rotacji, elementy macierzy ładunków W daj<| się łatwo interpretować. Współczynniki znaczące mają po rotacji wartości bliskie jedynce, natomiast mało znaczące są bliskie zeru. Obrotu dokonuje się zatem tak, aby ładunki przy cechach maksymalnie się różnicowały, wykorzystując warunek:

var w = Z (w_nnl - w,,)² - max .

Stosowna procedura realizująca opisaną rotację ortogonalną nosi nazwę metody varimax.

Przykład.

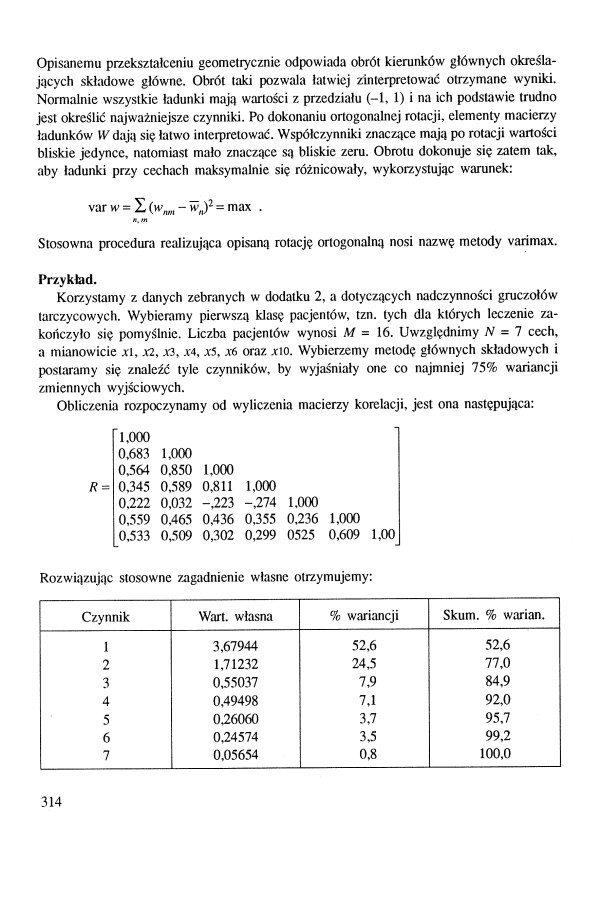
Korzystamy z danych zebranych w dodatku 2, a dotyczących nadczynności gruczołów tarczycowych. Wybieramy pierwszą klasę pacjentów, tzn. tych dla których leczenie zakończyło się pomyślnie. Liczba pacjentów wynosi M = 16. Uwzględnimy N = 1 cech, a mianowicie ati, X2, jt3, .v4, x5, x6 oraz ,rio. Wybierzemy metodę głównych składowych i postaramy się znaleźć tyle czynników, by wyjaśniały one co najmniej 75% wariancji zmiennych wyjściowych.

Obliczenia rozpoczynamy od wyliczenia macierzy korelacji, jest ona następująca:

1,000

0,683    1,000

0.564    0.850    1.000

R =

0,345    0,589    0,811    1.000

0.222    0,032    -.223    -.274    1,000

0,559    0,465    0,436    0,355    0.236    1,000

0,533    0,509    0,302    0,299    0525    0,609 1,00

Rozwiązując stosowne zagadnienie własne otrzymujemy:

Czynnik	Wart. własna	% wariancji	Skum. % warian.
1	3,67944	52,6	52,6
2	1,71232	24,5	77,0
3	0,55037	7,9	84,9
4	0.49498	7,1	92,0
5	0.26060	3,7	95.7
6	0,24574	3,5	99,2
7	0.05654	0.8	100,0

314