kww mdm3

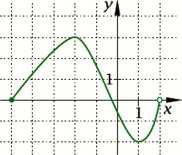
13. Które własności zostały zapisane poprawnie dla funkcji przedstawionej na wykresie obok?

ZESTAW ZADAŃ PRZYGOTOWAWCZYCH POZIOM PODSTAWOWY Zadania zamknięte (1 punkt)

1.    Dane są liczby:

x = |-2,8-(-0,3)1, y = |-0,3| - |-2,8|.

Która z liczb jest większa?

A.    y    C. obie są równe

B.    x    D. nie można tego określić

2.    Pierwszy pociąg jedzie ze średnią prędkością 60 a drugi - ze średnią prędkością 15 Który z tych pociągów'jedzie wolniej i o ile?

A. drugi pociąg o 45 ^    C. pierwszy pociąg o6y

B. drugi pociąg o6y    D. pierwszy pociąg o 11 s

3.    Cenę książki podwyższono o 25% i obecnie kosztuje ona 50 zł. O ile procent należy obniżyć nową cenę, aby otrzymać cenę początkowy?

A. o 25% B. o 5% C. o 20% D. o 10%

.    ,    72² - 8?

4. Liczba x -₅— przedstawiona w postaci po-

167

tęgi liczby 2 to:

A. 2² B. 27 C. 2# D. 2"7

5.    Dane są liczby: |y,    3, -0,25, 2², -fy. Paty' liczb,

w' których jedna jest odwTotnością drugiej, to:

A.    i oraz -0,25 i 2²

B.    3 i -jy oraz | i -0,25

C.    -j i 2² oraz -|p i 3

D.    2² i 5 oraz i 3

6.    Usuwając niewymierność z mianownika ułamka

73

-—^=, otrzymamy:

4+273 ^{r r}

A. 73 + 1,5 B. 4 + 273 C. 73-1,5 D. 4-273

7.    Jaki jest stopień wielomianu, który jest sumą dwńch wielomianów': jednego wielomianu stopnia szóstego i jednego wielomianu stopnia czwnrtego?

A. 9 B. 6 C. 3 D. 2

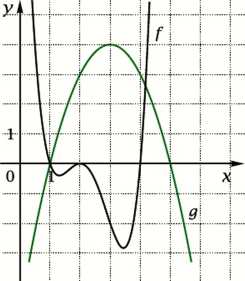
8. Na rysunku przedstawiono wykresy dwńch funkcji. Dla jakich argumentów' obydwie te funkcje jednocześnie przyjmują wartości dodatnie?

A.    x e (0; 1)

B.    x e (1; 4)

C. x e (4; 5)

D.    x e (5;+oo)

9. Wskaż zbiór rozwiązań nierówności |x + 3| >2.

A.

-i—i— B.	1-5-i-i-i-i-5-1- -3 0 2	—1—i—i-- X
	i \	, y, _
	-1 0	Ś X
C.
	0 1	5 x
D.
—	1—i—i—<(-—i—i—i—1-	—i—i—i-—

10. Mama jest obecnie trzykrotnie starsza od syna. Za 13 lat będzie już tylko dwmkrotnie starsza od niego. Ile lat ma obecnie mama?

A. 45 B. 54 C. 39 D. 36

11.    Wskaż parę prostych prostopadłych.

A.    y = 4x + 3 i -^x + 2y + 3 = 0

B.    y = 3x + l i —jx + y + 3 = 0

C.    y = -|x + 2 i -2x + 4y - 3 = 0

D.    y = 3x + 2 i x + 3y-l = 0

12.    Który z podanych punktów' leży na okręgu o równaniu (x - 2)² + (y + 4)² = 4?

A. (3,-4) B. (4,-4) C. (4,2) D. (-2,4)

A.    dziedzina: (-2; 3); funkcja rośnie w' przedziałach:

(-5; -2) i <1; 2)

B.    zbiór wartości: (-2; 3); funkcja rośnie w' przedziałach: (-5; -2) i (1; 2)

C.    dziedzina: (-5; 2); zbiór wnrtości: (-2; 3)

D.    funkcja rośnie w' przedziałach: (-5; -2) i (-2; 2) 14. Wykres funkcji opisanej w'zorem y = 2x² przesunięto o 2 jednostki w^r prawn oraz o 3 jednostki w' górę. Wzór otrzymanej funkcji ma postać:

A. y = 2(x + 2)² + 3    C. y = 2(x - 2)² - 3

B. y = 2(x - 2)² + 3    D. y = 2 (x + 3)² - 2 15. Funkcja kwadratowa y = 2x² - 5x + 8

A.    nie ma miejsc zerowych

B.    ma jedno miejsce zerowe

C.    ma dw⁷a miejsca zenwe

D.    ma trzy miejsca zerow'e

16.    W trójkącie równoramiennym ramię ma długość 6, a kąt przy podstawie ma miarę 30°. Wysokość podzieliła ten trójkąt na dwa trójkąty przystające. Obwód każdego z mniejszych trójkątów' jest równy:

A.    6 + 673    C. 9 + 373

B.    6 + 973    D. 9 + 673

17.    Człowiek o wproście 1,7 m rzuca cień długości 0,9 m. Kąt między promieniem słonecznym a podłożem ma miarę:

A.    ok. 27°    C. ok. 62°

B.    ok. 31°    D. ok. 90°

18.    Jak zmieni się średnia arytmetyczna liczb 7, 10, 11, 16, jeśli dopiszemy do tego zestawoi liczbę 21?

A. wyrośnie o 2    C. nie zmieni się

B. wyrośnie o 3    D. wyrośnie o 13

Zadania otwarte

19.    (2 pkt) W trójkącie prostokątnym krótsza przy-prostokątna ma długość 10, a sinus kąta ostrego leżącego przy dłuższej przyprostokątnej wynosi fj. Oblicz długości boków tego trójkąta.

20.    (3 pkt) Oblicz długość drogi, jaką przebędzie koniec w'skazów^rki minutowej zegara od godziny 12⁰⁰ do 13⁴⁰, wiedząc, że w'skazów^rka ta ma długość 10 cm.

21.    (4 pkt) W wielokącie foremnym liczba przekątnych jest trzy razy większa od liczby boków'. Obhcz miarę kąta wewnętrznego tego wielokąta.

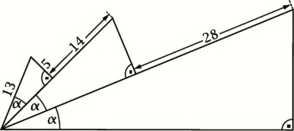
22. (4 pkt) Trzy trójkąty ułożono tak jak na rysunku. Oblicz pole największego trójkąta.

23. (4 pkt) W trójkąt równoramienny wpisano okrąg o promieniu 3 cm. Następnie narysowano drugi okrąg o promieniu 2 cm, który jest styczny do pierwszego okręgu i do ramion trójkąta. Obhcz pole trójkąta.

24. (5 pkt) Suma długości boku trójkąta i wysokości poprowadzonej do tego boku ma być równa 16. Jaką długość powinna mieć ta wysokość, aby pole trójkąta było możliwie największe? Jakie jest to największe pole?