1105139916

13

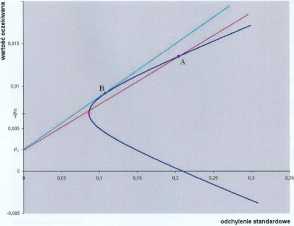
Rysunek 1.3. Graficzna interpretacja współczynnika Sharpe’a dla różnych portfeli.

na którym na pionowej osi widać punkt odniesienia - stopę bezryzykowną po i gdzie od razu widzimy, że portfel, którego obrazem, Markowitza jest punkt B, ma większy wskaźnik Sharpe’a niż np portfel, którego obrazem jest punkt A. Czy ten pierwszy (dający punkt B) nie ma przypadkiem największego możliwego, w jakiejś niesprecyzowanej jeszcze klasie portfeli, współczynnika Sharpe’a?

(Obraz Markowitza danego portfela - podstawowe pojęcie w teorii Markowitza - to punkt na płaszczyźnie R²(cr, E) mający współrzędne: odchylenie standardowe i wartość oczekiwana tego portfela. Będziemy systematycznie używać tego pojęcia już od Wykładu II. Czy czytelnik, odczytując optycznie dane z Rysunku 1.3, jest w stanie policzyć, według wzoru (1.1), przybliżone wartości wskaźników Sharpe’a tych portfeli, których obrazami Markowitza są punkty A i B ?)

Wracamy teraz do drugiego głównego przykładu dyskutowanego w tym wykładzie. Przyjmijmy (w nim), że obecnie no = 5%. Wtedy dla inwestycji w akcje spółki A wskaźnik Shar-pe’a wynosi °^qq⁰⁵ as 0.816. Natomiast dla naszego portfela x o minimalnym ryzyku mamy ^5%(^x) — ^287/7q80q ~ 0-579. Jest to wynik zdecydowanie słabszy!

Pozostaje jednak pytanie: czy jeżeli chcielibyśmy znaleźć portfel, dla którego współczynnik Sharpe’a przyjmuje wartość największą z możliwych (porównaj też Rysunek 1.3 powyżej), to czy właściwą odpowiedzią będzie ten złożony tylko z akcji „najlepszej” spółki? Otóż niekoniecznie! Często istnieje portfel „lepszy” i od portfela dającego najwyższą stopę zwrotu i od portfela

0    minimalnym ryzyku. Portfel taki ma wtedy stopę zwrotu znajdującą się pomiędzy stopami zwrotu powyższych dwóch portfeli i nazywa się go portfelem optymalnym ze względu na daną stopę zwrotu pozbawioną ryzyka. Okazuje się, że w tym przykładzie jest to x_op — (||, ^y)^T.

1    rzeczywiście, jego wskaźnik Sharpe’a wynosi około 0.818, odrobinę lepiej, niż dla portfela zawierającego wyłącznie akcje „najlepszej” spółki! W późniejszych wykładach, poczynając od dziewiątego, poznamy teorię dającą sposoby dochodzenia do takiego wyniku przy dwu lub też większej (dowolnej) ilości spółek w modelu.