Mechanika ogolna0015

30

Ruch występuje tylko na kierunku osi x,. Równanie drugie i trzecie są równaniami kinetostatycznymi, z których wyznaczamy reakcje podłoża działające na masę M.

Mamy więc odpowiednio:

Nj = P,

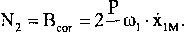
g

Widzimy, że reakcja N₂ zależy od prędkości względnej masy M. Podstawiając znane wielkości do pierwszego równania, dostaniemy:

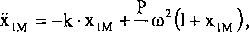
g

g

co po uporządkowaniu można zapisać jako:

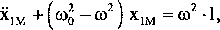
gdzie: co₀

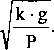
Jest to równanie opisujące ruch względny masy M. Rozwiązanie tego równania umożliwia określenie, jak przemieszcza się bryła 2 względem 1.

1.8. Równowaga względna

Równowaga względna masy wystąpi wówczas, gdy a_Mw = 0, czyli zgodnie ze wzorem (65):

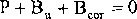
(68)

Zajmiemy się obecnie równowagą masy znajdującej się na Ziemi. Wiadomo, że Ziemia obraca się wokół własnej osi oraz przemieszcza się po orbicie dookoła słońca. Przy rozpatrywaniu naszego zagadnienia przyjmujemy, że ziemia wykonuje tylko ruch obrotowy wokół własnej osi.

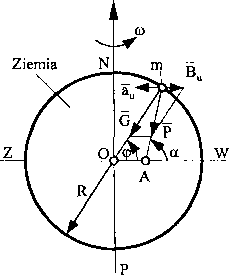
Ruch obrotowy Ziemi jest ruchem unoszenia dla każdej llltmy pnyoNlaiącej na Ziemi. 1’rędkość kątowa Ziemi wynosi: /tik hulamy, że masa umieszczona jak na rys. 15 nie przemieszcza się względem /Inni. Na masę działa siła przyciągania G skierowana do środka Ziemi. Dodatkowo tlziała jeszcze siła unoszenia wynikająca z obrotu Ziemi wokół własnej oni Silę tę określimy z zależności:

^Uu=-^m-a_u    (70)

2-TC

<i> =-

24-3600

rad

s

= const.

(69)

Rys. 15

Ci /yipicszenie unoszenia jest skierowane do osi obrotu Ziemi i wynosi:

n_n w²-R-coscp    (71)

Wntlość siły unoszenia wynosi: B_u =m-a_u =m-co² ■ R■ cos(p.Ponieważ v_w = 0, lo lównicż wartość siły Coriolisa jest zerem. Wypadkowa sił działających na nlinę w polu ziemskim to tzw. siła ciężkości masy, równa:

C (i + B_u    (72)

gd/te; I* siła ciężkości masy,

(I siła przyciągania ziemskiego,

B_u siła unoszenia.

/ powyższego wynika, że siła ciężkości masy i siła przyciągania Ziemi to dwie lózne siły. Widać więc, że limu dzliiliiniti siły ciężkości nic przechodzi przez modck Ziemi, ponieważ, u zip I loklnillile im biegunie siły ciężkości i przyeią-