Mechanika ogolna0030

60

Wektor K₀ pokazano na rys. 31.

^ZA

u

K₀ = K_z=K_zk

y

-►

Rys. 31

Zmianę krętu bryły w czasie określimy, wprowadzając równanie (118) do równania (98):

•Zj-Z;	yi) = -e-£mi-xi i=l	•^zi+®^2-£mj-yi i=l	■Zi =
[yz'®^2,
•Xi-Xi	n ■Zi) = -e-£^mi-yi i=l	n '^zi -©^2 • £m; -X; i=l	•^zi =
I.-C0^2,

n    n

k_z =Z^mi(^xi-z:-y,--(^xi ⁺y¹i)=\ ^E’

i=l    i=l

czyli:

K,=-I_łtt.e + I^-(D²=5;M_X(P₁)

i=l

K_y=-I„.e-I_]łł-(o²=^M_y(P_i)}.    (121)

i=l

K_z=I_z-e = XM_z(P_i)

i=l

Jeżeli opisujemy zjawisko obrotu bryły wokół osi z, to interesuje nas równanie: K_z = I_z-e = ][X(^Pi)’

umyli:

KV = ±M^)    022)

i=l

Hównanie (122) jest różniczkowym równaniem ruchu obrotowego bryły. Jeżeli

n    _

ukazałoby się, że ^M_z (P_;) = 0, to z równania (122) wynika, że K_z = I_z • (p = 0,

i=l

czyli:

K _z = I_z • co = const.    (123)

/.alrżność (123) to zasada zachowania krętu względem osi z. Wówczas prędkość

.    const.

kątowa co =-.

I_z

1'r/ykład 9

K i i|/,ck 1 hamulca klockowego, w momencie gdy obraca się z prędkością kąto-wt| (Do, zaczyna być hamowany stałą siłą P przyłożoną do dźwigni 2. Podać różniczkowe równania ruchu krążka, a następnie określić, po jakim czasie krążek ult; zatrzyma.

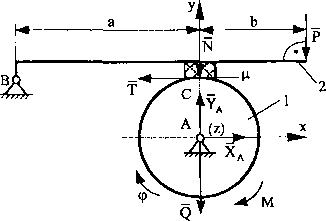
M moment działający na krążek [N-m], () nilu ciężkości krążka [N],

I’ nilu hamująca [N], i pi omień krążka 1,

n

f

wielkości geometryczne [m],

p współczynnik tarcia.

Wy*i. Iż

Kozpatrujemy ruch dynamiczny krążka. Przyjmujemy, że dźwignia pozostaje w równowadze statycznej. Ustalamy kierunek ruchu (przemieszczenie <p, tys. 32). Określamy siły zewnętrzne działające na krążek, czyli siły czynne I bierne. W punkcie styku krążku z dźwignią występują dwie reakcje składowe. Składowa normalna (reakcja N) oraz składowa styczna (siła tarcia T). Ponieważ jctil lo tarcic suche, zwrot siły tarcia jest przeciwny do założonego ruchu krążka.