Mechanika ogolna0082

Przykład 2H

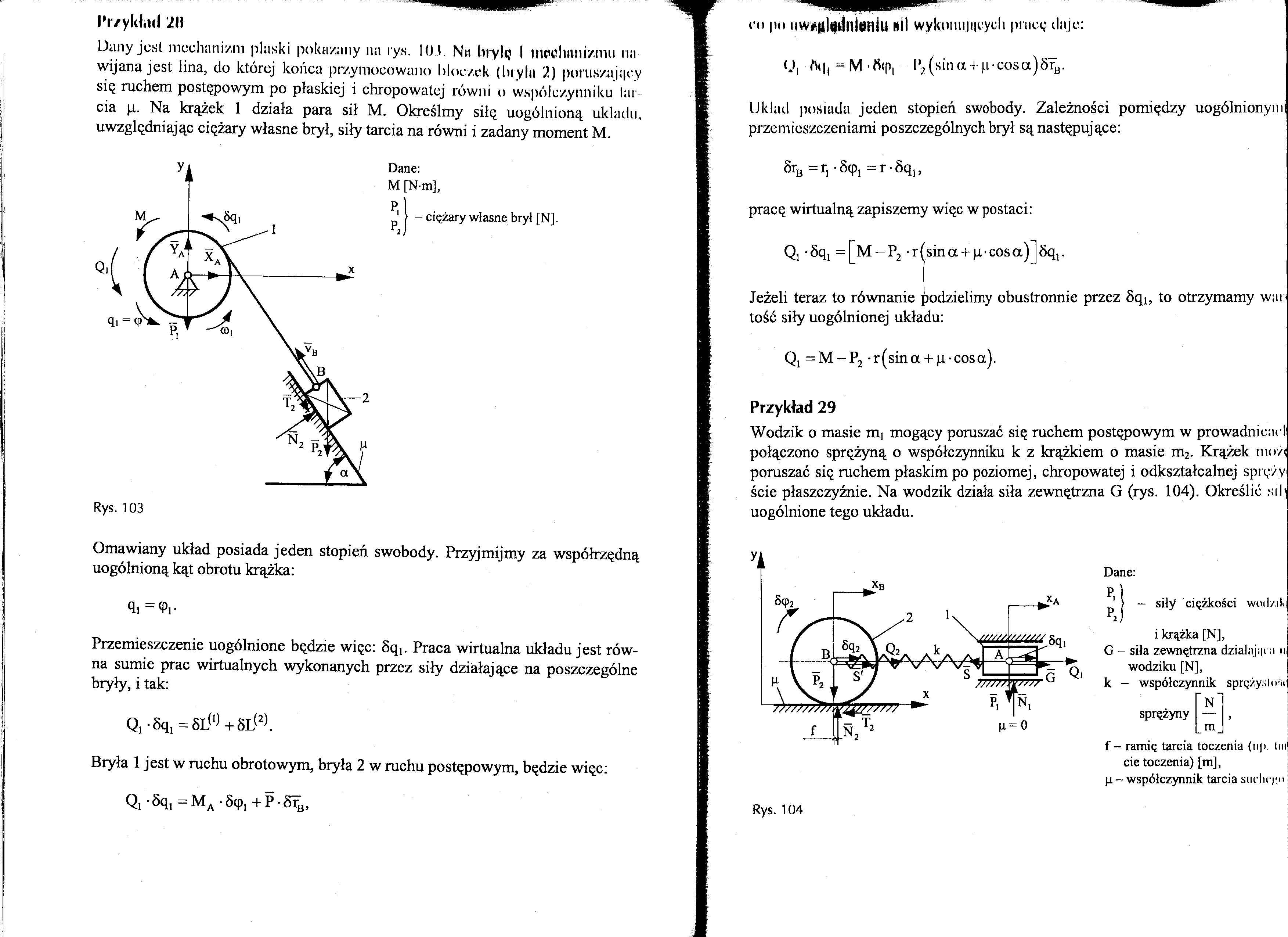
Dany jest mechanizm plaski pokazany na rys. 101. Ntt bryłę I uipclumizmu na wijana jest lina, do której końca przymocowano bloczek (bryki 2) poruszający się ruchem postępowym po płaskiej i chropowatej równi o współczynniku tarcia p. Na krążek 1 działa para sił M. Określmy siłę uogólnioną układu, uwzględniając ciężary własne brył, siły tarcia na równi i zadany moment M.

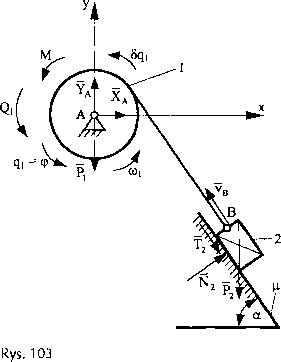
Dane:

M [N-m],

P,

- ciężary własne brył [N].

Omawiany układ posiada jeden stopień swobody. Przyjmijmy za współrzędną uogólnioną kąt obrotu krążka:

qi=<Pi-

Przemieszczenie uogólnione będzie więc: 8qi. Praca wirtualna układu jest równa sumie prac wirtualnych wykonanych przez siły działające na poszczególne bryły, i tak:

Q_r8q₅=8L^(I)+8L⁽²⁾.

Bryła 1 jest w ruchu obrotowym, bryła 2 w ruchu postępowym, będzie więc:

Oli po mwyltjilnmnlll Nl! wykoiiii|i|i'ydi pmcę daje: (.), rt«|j    P, (sin<x-l-|.i-cosa)5'Ęj.

Układ po,siada jeden stopień swobody. Zależności pomiędzy uogólnionymi przemieszczeniami poszczególnych brył są następujące:

8r_B=ri-8(p₁=r-Sq₁,

pracę wirtualną zapiszemy więc w postaci:

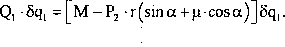
Jeżeli teraz to równanie podzielimy obustronnie przez Sq_b to otrzymamy w;u tość siły uogólnionej układu:

Q, =M-P₂ -r(sma + p-cosa).

Przykład 29

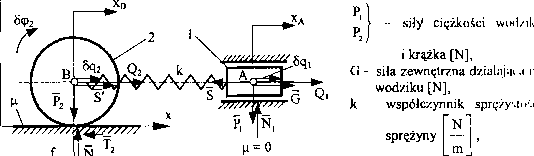
Wodzik o masie mi mogący poruszać się ruchem postępowym w prowadnicad połączono sprężyną o współczynniku k z krążkiem o masie m₂. Krążek mo/< poruszać się ruchem płaskim po poziomej, chropowatej i odkształcalnej spręży ście płaszczyźnie. Na wodzik działa siła zewnętrzna G (rys. 104). Określić silj uogólnione tego układu.

Dane:

f N.

i krążka [N],

G - sita zewnętrzna działająca n wodziku [N],

k - współczynnik sprężyslo-n "^N1

sprężyny — ,

[_m J

f- ramię tarcia toczenia (np. im cie toczenia) [m], p - współczynnik tarcia suclieyn

Rys. 104