Mechanika ogolna0069

138

Przykład 20

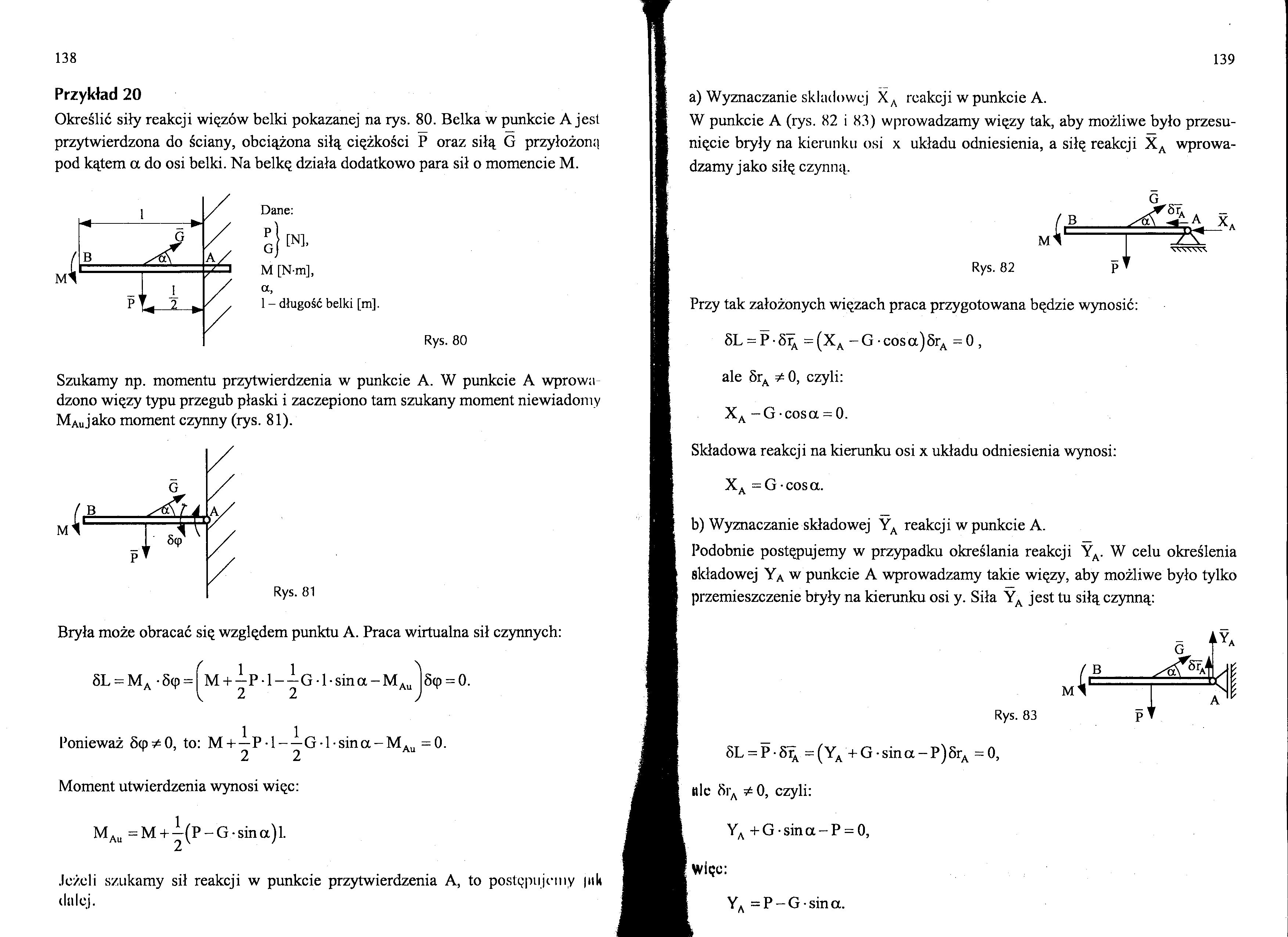
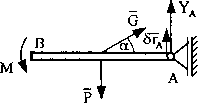
Określić siły reakcji więzów belki pokazanej na rys. 80. Belka w punkcie A jest przytwierdzona do ściany, obciążona siłą ciężkości P oraz siłą G przyłożona pod kątem a do osi belki. Na belkę działa dodatkowo para sił o momencie M.

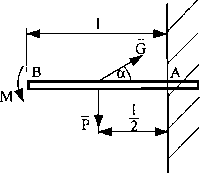
a,

1 - długość belki [m].

Dane:

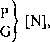
M [N-m],

Rys. 80

Szukamy np. momentu przytwierdzenia w punkcie A. W punkcie A wprowa dzono więzy typu przegub płaski i zaczepiono tam szukany moment niewiadomy M_Aujako moment czynny (rys. 81).

M

Sep

Rys. 81

Bryła może obracać się względem punktu A. Praca wirtualna sił czynnych:

8L = M_a • 8<p = | M + ^P-1—jG-l-sina-M_Au |8<p = 0.

Ponieważ 8<p^0, to: M + -^P-l-^-G-l-sina-M_Au =0. Moment utwierdzenia wynosi więc:

M_Au =M + ^(P-G-sina)L

Jeżeli szukamy sił reakcji w punkcie przytwierdzenia A, to postępujemy pik dalej.

a) Wyznaczanie składowej X_A reakcji w punkcie A.

W punkcie A (rys. 82 i 83) wprowadzamy więzy tak, aby możliwe było przesunięcie bryły na kierunku osi x układu odniesienia, a siłę reakcji X_A wprowadzamy jako siłę czynną.

G

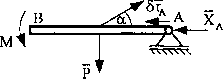
Rys. 82

Przy tak założonych więzach praca przygotowana będzie wynosić:

8L = P-8r_A = (X_A-G-coscx)8r_A =0, ale 5r_A * 0, czyli:

X_A-G-cosa = 0.

Składowa reakcji na kierunku osi x układu odniesienia wynosi:

X_A =Gcosa.

b) Wyznaczanie składowej Y_A reakcji w punkcie A.

Podobnie postępujemy w przypadku określania reakcji Y_A. W celu określenia składowej Y_A w punkcie A wprowadzamy takie więzy, aby możliwe było tylko przemieszczenie bryły na kierunku osi y. Siła Y_A jest tu siłą czynną:

Rys. 83

8L = P-8^ = (Y_A + G • sin a - P) 8r_A = 0, ale 8r_A s* 0, czyli:

Y_a + Gsina-P = 0,

Więc:

Y_a =P-Gsina.