img029

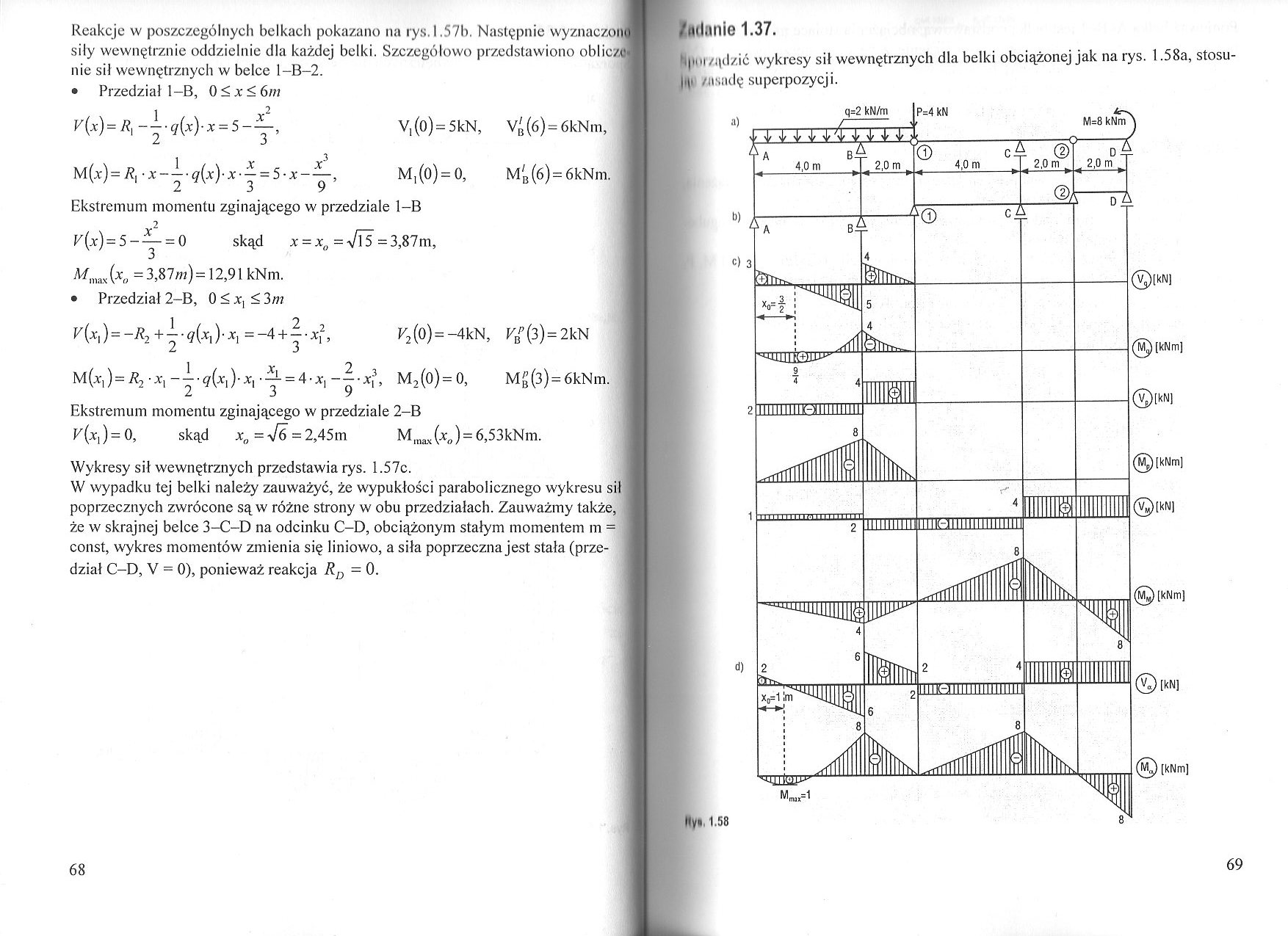
Reakcje w poszczególnych belkach pokazano na rys.I.57b. Następnie wyznaczom siły wewnętrznie oddzielnie dla każdej belki. Szczegółowo przedstawiono oblicz nie sił wewnętrznych w belce l-B-2.

• Przedział 1-B, 0<x<6m

V(x)=R_i-jq(x)-x = 5-y,    V,(o) = 5kN,    V'(6) = 6kNm,

Mj(0) = 0,    M'_B(6) = 6kNm.

M(x)=R_rx-~q(x)-x~ = 5-x-^-

Ekstremum momentu zginającego w przedziale 1-B

2

F(x) = 5- — = 0    skąd x-x₀-■Jis =3,87m,

3

M_nax (x₀ = 3,81 ni) = 12,91 kNm.

• Przedział 2-B, 0 < jc, < 3m

V{x, ) = ~R₂+j q{x_x)-x_x =~4 + jxf,    V₂ (o) = -4kN, Vf (3) = 2kN

M(^,) = /?₂-x,-^-q(x_x)-x_x ~ = 4-x_x -^-x_x, M₂(0) = 0,    M_b(3)-6kNm.

Ekstremum momentu zginającego w przedziale 2-B

V(x_x) — 0, skąd x₀ = Vó =2,45m M,_nax(x₀) = 6,53kNm.

Wykresy sił wewnętrznych przedstawia rys. 1.57c.

W wypadku tej belki należy zauważyć, że wypukłości parabolicznego wykresu sił poprzecznych zwrócone są w różne strony w obu przedziałach. Zauważmy także, że w skrajnej belce 3-C-D na odcinku C-D, obciążonym stałym momentem m = const, wykres momentów zmienia się liniowo, a siła poprzeczna jest stała (przedział C-D, V = 0), ponieważ reakcja R_D — 0.

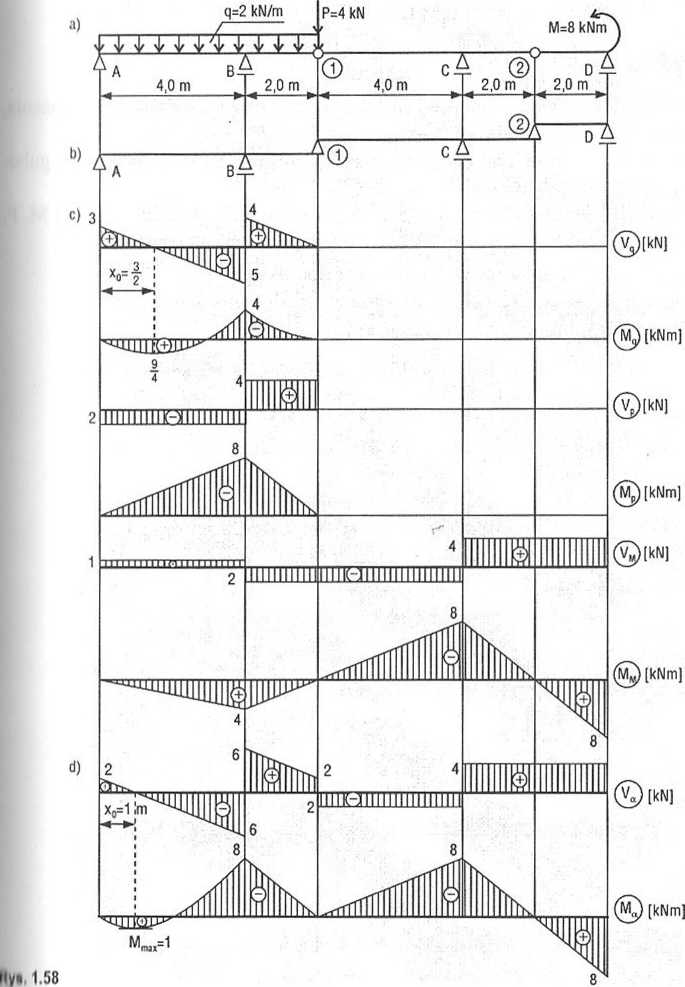
/mianie 1.37.

/,i)il/ić wykresy sił wewnętrznych dla belki obciążonej jak na rys. 1.58a, stosu-m /nsiulę superpozycji.

69