Mechanika ogolna0004

1. DYNAMIKA PUNKTU MATERIALNEGO

1.1. Siły działające na punkt materialny

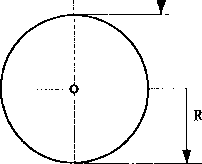
Siły te możemy podzielić na czynne i bierne (siły reakcji). Wśród sił czynnych jest zawsze siła przyciągania ziemskiego, bo wynika to z faktu, że punkt materialny, którego ruch opisujemy, znajduje się w polu ziemskim. Przyjmujemy, że Ziemia jest kulą o promieniu R i masie M. Natomiast punkt materialny M, którego masa jest równa m, znajduje się w odległości h od powierzchni Ziemi (rys. 3).

VQ

h

R

m - masa punktu materialnego

R- średni promień kuli ziemskiej ~ 6370 [km]

Rys. 3

Masy M i m oddziałują na siebie siłami takimi samymi co do wartości, skierowanymi wzdłuż prostej łączącej te punkty. Wartość siły wzajemnego oddziaływania oznaczymy przez Q. Siłę tę, z jaką Ziemia oddziałuje na każdą masę m umieszczoną w polu ziemskim, nazywamy siłą przyciągania ziemskiego. Jej wartość można zapisać w postaci:

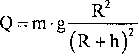
Załom siła przyciągania jest co do wartości odwrotnie proporcjonalna do kwadratu odległości masy od środka Ziemi. Jeżeli opisujemy ruch masy m w niewielkiej odległości od powierzchni Ziemi, to h«R i wówczas przyjmujemy, że:

(4)

Q = m • g = const.

Sili,- tę praktycznie przyjmuje się jako siłę ciężkości masy.

/ podanej zależności określamy masę:

m = — = const.    (5)

g

gdzie: Q - wartość siły przyciągania ziemskiego [N],

m - masa punktu materialnego pozostającego w polu ziemskim [kg],

g

m	II s>° OO	m	~ 10	m
		~T		2
Ls J		_s J		Ls J

- średnie przyspieszenie ziemskie, które

w różnych punktach na powierzchni Ziemi jest różne, przyjmowane jako równe 10 —.

l ale więc dwie masy: mi i m₂ mająróżne ciężary:

(6)

Q, =m, -g

Q₂ = ^m2 ' g

ili|d iloraz ciężarów jest równy stosunkowi ich mas:

⁽.>i m,

(.),    m ₂

1.2. Różniczkowe równania ruchu punktu materialnego

Nu punki materialny M działa układ sił (czynnych i sił reakcji) P! ... P_n (rys. 4), i żyli na masę działa siła wypadkowa W :

W I* £l>

i-i

(7)