Mechanika ogolna0034

68

Moment bezwładności krążka: I_A =—m-r =-r . Po podstawieniu do rów-

2-g

nań ruchu:

(1)-x_a=G-T,

g

(2)    —r²-ćp = T-r-P-f,

2g

(3)    x_A = r - <p.

Rozwiązujemy powyższy układ równań w następującej kolejności: Z drugiego równania wyznaczymy siłę tarcia:

f P

(4) T=P—+- x_A, r 2 ■ g

wstawiamy do pierwszego i mamy: f P ..

P .. g

x_a=G-P-

2_

■g

1’rzyspieszenie środka masy krążka będzie więc wynosiło:

2(G-r-P-f)

X _A =—-^L%-

3-P-r

Po scałkowaniu dostaniemy prędkość środka masy krążka: .    2(G • r - P • f)

3P-r

-g ■ t + Cj.

Kolejne całkowanie pozwoli wyznaczyć przemieszczenie środka masy bryły w funkcji czasu:

2(G - r - P • f)    ₂    ^

- ^V -^Zg t² + C, -t + C₂.

3-P-r

/uldadamy zerowe warunki początkowe, tzn. dla t₀=0, x_A=0, x_A = 0. Uwzględniając to w powyższych równaniach, dostaniemy wzory opisujące ruch Al odka masy krążka:

(5)

X_A =

2(G-r-P-f)

3-P-r

2(G-r-P-f)

3-P-r

2(G-r-P-f)

3-P-r

8,

g’U

g-t^z

lóndck masy będzie przemieszczał się jak założono, jeżeli dla dowolnej chwili i /iisu prędkość x_A > 0, czyli: G • r - P • f > 0, tzn. że wartość siły wymuszają-

f

n'l ruch musi spełniać warunek G >P—. Określimy jeszcze wartość siły tarcia

r

'uii hcgo z równania (4). Znamy przyspieszenie środka masy krążka, więc siła lun ia będzie wynosić odpowiednio:

g,

_{T r}f_| P 2(G-r-P-f) r 2•g 3-P-r

i u po uproszczeniu daje:

r = *pI₊io.

3 r 3

Wnulomo, że siła tarcia suchego nie może być większa od tarcia rozwiniętego, ożyli:

T < p • N,

i i > w analizowanym przypadku daje:

2    f 1

_jP- + -G<p-P,

3    r 3

nli|il:

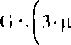
r

P.