P21m jpeg

International Tables for Crystaliography (2008). Vol. A, Space group 11, pp, 164-167.

P2,/m    2/m    Monoclinic

No. 11    P\2y/m\    Patterson symmetry P12/m 1

UNIQUE AXIS b

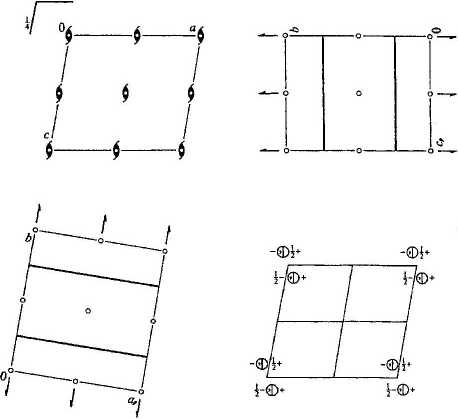
Origin at I on 2,

Asymmetric unit 0 < x < 1; 0 < y < *; 0 < z < 1 Symmetry operations

(1) 1    (2) 2(0,5,0) 0,y,0    (3) I 0,0,0    (4) m xĄ,z

Generatora selected (1); *(1,0,0); *(0,1,0); *(0,0,1); (2); (3)

Positions Multiplicity, Wyckoff letter, Site symmetry		Coordinates
4 / 1	(I)W	(2)J,y + i? (3)x,y,l,
2 e m	x,j,z	X,3,Ź
2 !	ł,o, i
2 c !	0,0, i	0,5,3
2 b I	*,0,0	3,3,0
2 o 1	0,0,0	0,3,0
Symmetry of special projections
Along [001] p2gm a' = a. b' = b Origin atO, 0 ,z		Along [100] p2mg a' = b b' = c Origin atx,0,0

CONTINUED

No. 11

P2jm

Refiection conditions General:

(4) x,y + {,z    0&0: k = 2n

Special: as above, plus no extra conditions hkl : k = 2n hkl : k=2n hkl : k = 2n hkl : k — 2n

Along [010] p2 a' = c b' = a Origin at 0,y,0

Maximal non-isomorphic subgroups

I	[2] P1 m 1 (Pm, 6)	1; 4
	[2]P12,\(P2l,4)	i; 2
	[2]Pi (2)	1; 3
Ha	nonę
II b	[2]PI2,/cl (c^1 = 2c)(P2,/c, 14); [2]P12,/cl (a' = 2a)(P21/c, 14); [2]S12,/el (a’= 2a,c'= 2c)(P2,/c, 14)

Maximal isomorphic subgroups of lowest index

Dc [2] P12,/m 1 (c* = 2c or a' = 2a or a' = a + c, t~-a + c) (P2Jm, 11); [3] P12,/m 1 (b' = 3b) (P2,/m, 11)

Minimal non-isomorphic supergroups

I    [2] Pmma (51); [2] Pbcm (57); [2] Pmmn (59); [2} Pnma (62); [2]Cmcm (63); [3] P6_}/m (176)

II    [2] C12/m 1 (C2/m, 12); [2] A12/m 1 (C2/m, 12); [2] /12/mI (C2/m, 12); [2]PI 2/ml (b' = |b) (P2/m, 10)

165