skanuj0033

64

Ruch będzie odbywał się nadal, gdy k_xę_x > M_r W przeciwnym przypadku ciało zatrzyma się w położeniu określonym kątem <p_l.

Załóżmy, że ruch odbywa się nadal. Opisany jest drugim równaniem (14), ponieważ teraz (p<0. Jeżeli czas zaczniemy liczyć od chwili rozpoczęcia tego etapu ruchu, to warunki początkowe są następujące:

(21)

<p{V) = ę, , <p(Q) = 0

Postępując podobnie jak poprzednio otrzymamy rozwiązanie postaci:

(22)

Powyższe wyrażenie opisuje ruch do czasu t₂, w którym prędkość kątowa ciała równa się zeru. Na podstawie (22) otrzymujemy:

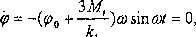
(23)

a stąd, podobnie jak poprzednio, obliczamy t₂ =—. Zatem czas ruchu w

co

prawo i w lewo jest jednakowy. Czas potrzebny na jedno pełne drganie nazy-

2tc

wany jest okresem drgań; jego wartość: T +t₂ - —. Okres ten jest więc

co .

równy okresowi drgań nie tłumionych (5).

jednego drgania kąt maksymalnego wychylenia maleje o stałą wartość:

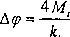
(24)

Stąd wynika, że kąt maksymalnego wychylenia („amplituda”) maleje liniowo w zależności od czasu.

Jeżeli zachodzi nierówność: k_{\ę₂\ > M,, to ruch odbywa się nadal i przedstawione rozwiązanie można kontynuować. Po skończonej liczbie wahnięć analogiczna nierówność nie jest spełniona i ciało zatrzymuje się na stałe.

Obecnie przechodzimy do opisu drgań tłumionych wiskotycznie. Obliczymy odstęp czasu pomiędzy kolejnymi skrajnymi wychyleniami ciała. Ekstremalne wartości kąta ę wyznaczamy przyrównując do zera prędkość kątową, obliczoną na podstawie wzoru (9):

ę =    sin (cy,/ + e) +    cos (aj + s) - 0.    (25)

Stąd otrzymujemy:

tg(<V+ *) = -?-.    (26)

o

Oznaczmy przez /„ najmniejszy nie ujemny pierwiastek powyższego równania trygonometrycznego. Wówczas pozostałe, dodatnie pierwiastki tego równania są:

/„=*„+ — , n = 1,2,3,...    (27)

®i

W chwilach t_n ciało osiąga skrajne położenia. Zgodnie z (27) czas, który upływa między dwoma kolejnymi skrajnymi wychyleniami (w przeciwne strony) wynosi n/co_l . Okresem drgań nazywamy czas potrzebny na jedno

pełne drganie; zatem okres drgań wynosi 7J=— .

0)\

Obliczymy ekstremalne wychylenia ciała podstawiając do (9) chwile t_H dane wzorem (27):

=    sin(a>jf₀ +nn + e)~ (-l)"®_m e^-5'" ,    (28)

gdzie wprowadzono oznaczenie: O_m = Osin(a>it₀ +s), n = 0, 1,2, .... Zatem ekstremalne wychylenia ciała są na przemian dodatnie i ujemne (znajdują się po obydwu stronach położenia równowagi), a ich wartości maleją wykładniczo w zależności od czasu. Maksymalne wychylenia po jednej stronie położenia