skanuj0064

sporządzenie uproszczonego wykresu zmęczeniowego Smitha oraz wyznaczenie współczynnika bezpieczeństwa na zmęczenie dla przykładowego cyklu naprężeń zmiennych.

6.3. OBCIĄŻENIA I NAPRĘŻENIA OKRESOWO ZMIENNE

Najprostszym przypadkiem okresowo zmiennego obciążenia jest przypadek działania osiowej siły P, której wartość jest harmoniczną funkcją czasu t. Siła ta da się określić wzorem:

P = P_flsin(cuf) N,

gdzie P_a N jest amplitudą siły, co s“¹ — częstością kołową zmian tej siły. Okres zmian wartości siły wynosi

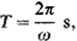
I

T

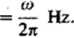
a częstość zmian

v

Jeżeli n oznacza liczbę okresowych zmian zachodzących w ciągu 1 min, to

Jeśli pod wpływem działania tak zdefiniowanej siły w obciążonym elemencie wystąpi jednoosiowy stan napięcia, to wartość głównego naprężenia normalnego zmieniać się będzie według zależności:

a = <j_a sin(u>f),

w której |orJ określa tzw. amplitudę naprężenia. Naprężenie a zmieniać się zatem będzie okresowo w zakresie od — + c_a do a_mui — — symetrycznie względem zera. Takie naprężenia nazywać będziemy wahającymi lub oscylującymi, a przebieg ich zmian w czasie określa sinusoida (rys. 6.1). Jedną zmianę naprężenia od wartości np. do najbliższej tej samej wartości o_mAX nazywamy cyklem, a czas tej zmiany mierzony w sekundach — okresem T. W przypadku dowolnego, lecz okresowego przebiegu zmian naprężeń, wartości naprężeń są w każdej chwili inne, lecz zawsze zawarte między i Przebieg ich zmian można zatem przedstawić również w postaci sinusoidy (patrz rys. 6.2), której oś wyznaczona będzie przez średnie naprężenie cyklu wynoszące

<*m

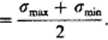
87