skanuj0070

140

140

(4.7)

(4.8)

dę₌_jw_

dr ^+^,1+^,2

Przyrównując stronami (4.6) i (4.7) otrzymujemy równanie: T.-T    dT

---= cm—.

Rk^+Rsi⁺R, 2

Po rozdzieleniu zmiennych w równaniu (4.8) i wycałkowaniu go dostajemy, że różnica temperatur pomiędzy grzejnikiem a odbiornikiem zanika w czasie według wzoru:

__T_

AT - AT_Q e (^RSl+Ksi+K_t)cm _

Gdy powierzchnie grzejnika, odbiornika oraz próbki są polerowane, a badany materiał jest izolatorem cieplnym, wówczas mamy podstawy, aby przyjąć, że:    ¹

|    Rsi ⁺ Rs2 « R/c

i wówczas:!

AT s AT₀ e’    = AT₀ e* ^r“ .    (4.9)

Literatura!

i

[1]    S.Wiśniewski: Wymiana ciepła. PWN, Warszawa 1979.

[2]    M.Hering: Termokinetyka dla elektryków. Wydawnictwo Naukowo-Techniczne, Warszawa 1980.

Ćwiczenie 11 ¹

Wyznaczanie równoważnika elektrochemicznego wodoru i miedzi

1. Wprowadzenie

Substancje o wiązaniu jonowym lub cząsteczki polarne (niektórych kwasów, zasad i soli) rozpuszczane w cieczy o dużej względnej przenikalności elektrycznej (np. w wodzie o e_r = 81) ulegają rozpadowi na jony, czyli dyso-cjacji elektrolitycznej. Roztwory takie nazywamy elektrolitami.

Rozpad cząsteczek obojętnych na jony następuje w wyniku oddziaływania na te cząsteczki dipolowych cząsteczek wody, co prowadzi do rozerwania wiązań chemicznych (patrz rys.l, ćw.15).

W elektrolitach, równolegle do dysocjacji, przebiega proces rekombinacji jonów. W wyniku tych procesów ustala się równowaga dynamiczna pomiędzy liczbą cząsteczek rozpadających się i powstających. W roztworze istnieje zatem pewien stopień dysocjacji a, określony jako stosunek liczby moli cząsteczek zdysocjowanych n, do ogólnej liczby moli cząsteczek n₀ zawartych w roztworze:

(1)

n

a - —

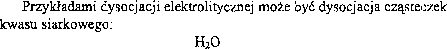
H₂S0₄    2H⁺ + S0₄”,.

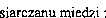
(2)

(3)

Cu SO4 <-    '^>- Cu⁺⁺ + SO4

1

Opracował A.Kubisz.