skanuj0097

ii yc/.ncgo, równoległego do kierunku przepływu prądu.

Aby zrozumieć to zjawisko, przyjmijmy, że nośniki prądu w próbce przewin lżącej (niech będą to elektrony), można uważać za swobodne. Oczywiście |i-ii lo pewien model fizyczny, a więc idealizacja rzeczywistości.

Zakładamy, że w przypadku nieobecności pola magnetycznego wszystkie elektrony poruszają się ze średni ^prędkością unoszenia v w kierunku prze-i iwnyni do pola elektrycznego E (rys.2).

I

d

qvxB

E = E_xi

v

qE_H

+ + + +++ +

I

x

ŻZh    /5

Kys.2. Siły działające na nośniki prądu o ładunku ujemnym w zjawisku Halla. Pole

magnetyczne o indukcji B skierowane jest poza płaszczyznę rysunku. Natężenie prądu elektrycznego wynosi I. Prędkość unoszenia nośników prądu jest równa v

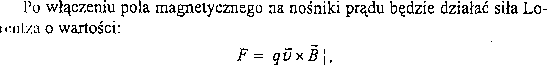
skierowana prostopadle do ich prędkości v i do wektora indukcji B. Siła ta będzie zakrzywiać tor cząstek. Wskutek tego na jednym z boków próbki wy-Iworzy się nadmiar elektronów i bok ten naładuje się ujemnie, a na przeciwnym boku pozostaną jony dodatnie. Powstanie pole elektryczne E_H prostopadle do kierunku przepływu prądu, a zatem pojawi się siła elektrostatyczna ■(l' n skierowana przeciwnie do kierunku działania siły Lorentza. Siła elektro-iiniyuzna będzie narastać, dopóki nie zrówna się co do wartości z siłąLorent-,u Wtedy wpływ obu sił na ruch nośników skompensuje się.

Rozważając warunki powstałej równowagi (patrz: Uzupełnienie) otrzymujemy następujące wyrażenie na napięcie Halla U_H:

, (1)

nq h    n

gdzie: n oznacza koncentrację nośników prądu o ładunku q,h- grubość próbki (patrz rys.2), I - natężenie prądu przepływającego przez próbkę, B - wartość indukcji pola magnetycznego. Stała Rh = 1 /nq jest nazywana stałą Halla.

Wzór (1) daje na ogół bardzo dobrą zgodność z doświadczeniem, chociaż, jak wspomnieliśmy, opiera się na prostym modelu i nie uwzględnia innych efektów towarzyszących zjawisku Halla, których omówienie przekracza ramy niniejszego opracowania.

Jak widać, znak stałej Halla zależy od znaku nośników prądu, W przypadku elektronów q = -e, co daje R_H <0 .

Dla niektórych materiałów otrzymujemy jednak dodatnią wartość R_H. Mówimy wtedy o anomalnym efekcie Halla. Tłumaczymy go obecnością w próbce dodatnich nośników prądu - dziur. Dokładniejsze informacje na ten temat można znaleźć w literaturze [1],

Ważnym parametrem jest ruchliwość nośników u. Wielkość tę definiujemy jako współczynnik proporcjonalności między wartościami prędkości nośników i natężenia pola elektrycznego w próbce:

v — u ■ E.

W wielu ciałach występują zarówno elektrony jak i dziury. Dokładniejsze rozważania uwzględniające ten fakt prowadzą do następującego wzoru na stałą Halla:

_n ~nk} + p

—    7* i

e{nk + p)

gdzie: k ~uju_p oznacza stosunek ruchliwości elektronów do ruchliwości dziur, n - koncentrację elektronów, p - koncentrację dziur.

Eksperymentalne wyznaczanie stałej Halla pozwala uzyskać informacje m. in. o koncentracji nośników prądu, określić ich typ i ruchliwość.