skanuj0117

232

Zadanie 5

Przeprowadzić obserwację krzywych Lissajous (więcej na temat tych krzywych znajdziesz w Uzupełnieniu).

Jeżeli złożymy dwa wzajemnie prostopadłe drgania harmoniczne o jednakowych, dla uproszczenia, amplitudach opisane równaniami:

x = a cos a)_xt, y = acos((O_yt + <p),

to dla szczególnych relacji między częstościami a>_x i a>_y oraz dla specjalnie dobranych różnic faz ę otrzymujemy krzywe Lissajous przedstawione na rys. 16 w Uzupełnieniu.

1.    Łączymy obwód według schematu przedstawionego na rys.lOa lub lOb. Na płytki odchylania pionowego oscyloskopu podajemy napięcie U_y z generatora sygnału G\, zaś na płytki odchylania poziomego - napięcie U_x z drugiego generatora G₂ (rys.lOa) lub napięcie z sieci (rys. 1 Ob). G\ posiada dodatkowo' wmontowany częstościomierz pozwalający na pomiar częstotliwości sygnału, PP jest to tzw. przesuwnik fazowy, umożliwiający zmianę fazy sygnału z generatora G₂.

Zmieniając'stosunek częstości sygnałów U_xiU_y: — = 7 ;    ; ~ ;...

o)_x 12    3

i fazę ę - 0, f ,y... obserwujemy pojawiające się na ekranie krzywe Lissajous i za każdym razem przerysowujemy je na papier milimetrowy.

2.    Ustalamy częstość i zmieniamy częstość aiy tak, aby na ekranie oscylo-

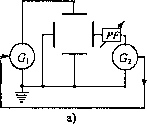
Rys.10. Schematy obwodów elektrycznych do obserwacji figur Lissajous

skopu uzyskać wyraźną krzywą Lissajous, którą przerysowujemy ją na papier milimetrowy.

Z kształtu dowolnej nieruchomej krzywej Lissajous można określić stosunki częstości drgań harmonicznych, które wykonuje punkt drgający w kierunkach osi x i y. W tym celu przecinamy krzywą Lissajous prostą równoległą do osi x i liczymy liczbę N_x punktów przecięcia prostej z krzywą (punkty przecięcia, przez które krzywa Lissajous przechodzi dwa razy, liczymy podwójnie). Podobnie postępujemy dla prostej równoległej do osi y. Stosunek częstości wyraża się przez odpowiednie liczby punktów przecięcia wzorem:

(1)

o\_N_ł o_y ~ N_x

Ze wzoru (1) wynika metoda znajdowania nieznanej częstości sygnału, jeśli znamy drugą częstość, np. C0x oraz krzywą Lissajous.

Zapisujemy C0x oraz N_x i N_y w tabeli 2, następnie wyliczamy:

Wy = NX(DX/ Ny .	Lp.	co*		Ny
Wynik ten również wpisujemy do tabeli 2.

3. Uzupełnienie

3.1. Figury Lissajous

Krzywą (figurą) Lissajous nazywamy tor, jaki zakreśla punkt .drgający harmonicznie w dwóch wzajemnie prostopadłych kierunkach. Ogólne: równania krzywej Lissajous, w których parametrem jest czas, mają postać:

x = acos(o)_xt + <p_x) y = bcos(o}_y^ + ^)_y)^,

gdzie a i b oznaczają amplitudy drgań odpowiednio w kierunkach 'osi x i y, co_x i co_y to częstości a ę_x i ę są fazami początkowymi tych drgań.

Załóżmy, że ę_x - 0, (p_y=<p i częstości obydwu drgań są jednakowe, tzn. x = a cos cot y = bcos(a>t + <p).