skanuj0161

320

W Ą

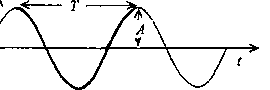
a) ^l'x ustalone ■    y/(t) = Asm(2nft+<p)

L

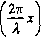
b) ustalone ' yr(x) = A sin

W

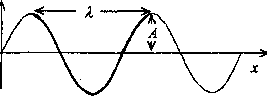
Rys.3. Falą harmoniczna rozchodząca się wzdłuż osi x. a. Wychylenia ustalonego ele-' mentu ośrodka x w czasie maję postać drgań harmonicznych prostych, T- okres drgań, A - amplituda, b. W ustalonej chwili czasu / pokazano kształt fali wzdłuż osi x, 2- długość fali.

Należy ipodkreślić, że w falach mechanicznych przez ośrodek przesuwa się zaburzenie, i nie sama materia, której cząstki wykonują jedynie drgania wokół położeń równowagi. Ponieważ z ruchem cząstek związana jest energia kinetyczna i potencjalna, więc rozchodzenie się drgań oznacza transport energii przez falę.

1.2. Superpozycja fal

Fale mogą przebiegać w danym ośrodku niezależnie od siebie, co oznacza, że w danej chwili czasu przemieszczenie dowolnej cząstki jest sumą przemieszczeń wywołanych przez każdą z fal.

Rozważmy przypadek nakładania się dwóch fal o jednakowych amplitudach, rozchodzących się w przeciwnych kierunkach. Z sytuacją taką mamy do czynienia przy odbijaniu się fal na przeszkodach (rys.4a). W wyniku superpozycji fali padającej na przeszkodę z falą odbitą dostajemy falą stojącą (rys.4b). W przypadku padania na ośrodek gęstszy następuje skok fazy ę fali odbitej o n

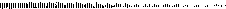
fala padająca

lilii

gdzie n = 0, 1,2,...

fala odbita

Bee

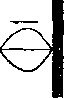
Rys.4. a. Fala padająca i odbita od ośrodka gęstszego, b. Obwiednia fali stojącej powstającej w wyniku nakładania się fal z przypadku a

(odpowiadający połowie okresu). Natomiast przy odbiciu od ośrodka o mnie szej gęstości faza ę nie ulega zmianie.

Napiszmy równania obu fal, podającej i odbitej, rozchodzących się wzdł osi x w przeciwnych kierunkach:

i//_l(x,t) = Asm(kx-ć)t + <p₁) i y/₂(x,t)~ Ańa(kx + cot + ę₂)-

Dla uproszczenia przyjmijmy ę>\ = 0 oraz <pi = n. Fala wypadkowa będzie tych fal:

y/(x, t) = y/\ (■*, 0 +1^2 (*> t) = Asm (kx- tut) + A sin (kx + cot + tu) . Przekształcając powyższe wyrażenie¹ dostaniemy równanie fali stojącej:

\j/{x, t) = 2 A cos (kx) cos (cot + rc/2).

amplituda

Ze wzoru (3) wynika, że każda cząstka drga prostym ruchem harmonicznym] częstość drgań jest taka sama dla wszystkich cząstek. Wyrażenie 2Acos(Ja) od| grywa tu rolę, zależnej od położenia i charakterystycznej dla fali stójącej, am| plitudy drgań. W punktach zwanych strzałkami i spełniających warunek:

fce=(2n + l)— czyli x-(2n + l)—, 2    4

1

Korzystamy m.in. ze związku trygonometrycznego: sin a + sin ^ = 2 sin ° ^ cos--