Scan10031

PRZYKŁAD i- y"-y'=o r²-r=0

r(r-l)=0-^r₁=0->e^0x=i=y_ł, r₂=l-»e^x=y₂ y=Ci+C₂e^x c.o.r.l.j.

2.2y"+y=0

2r^+l=0-4.

-J2

y = C, cos—

r,

- I V 2

■ + sm —x 9

a = 0

2

.>1

jf

y₂

. -sil = sm—x 9

c.o.r.i.j.

3. >"-2y'+y=0 r²-2r+l=0

.'-l)‘=0-^r₁=r2=r=i->y₁=e^xAy2=xe^x v=C_:e^x-r C₂xe^x c.o. r. I. j.

Równanie różniczkowe liniowe Ii-go rzędu rozwiązujemy w Il-ch etapach . W r I jednorodne, a w II-gim metodą uzmienniania stałych wyznaczamy Ci(x)i C₂(x). Sca^e te wyznaczamy z układu równań, w którym występują, one jako pochodne, jeżeli więc w całce ogólnej r.l.jednorodnego uzmiennimy stałe to otrzymamy: y =C_l(x)-y_l + C₂(x)-y₂

18

• }\ + C₂'(x) -y₂ =0 • yM f(x)

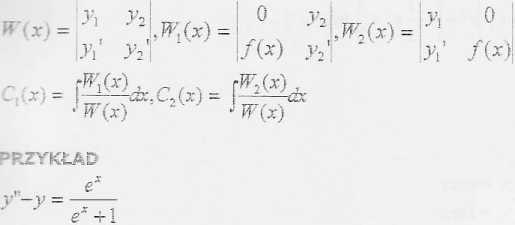
I    etap y"-y=0

r²-l=0->r_a=l->e^x

r₂=-l->e"^x

y=Cie^x+c₂e'^x c.o.r.l.j.

II    etap Ci-fC₁(x), C₂-»C₂(x)

y = C\(x)e^x +C₂(x)e~^x

C_x'(x)e^x + C₂'(x)e~^x = 0

19