Scan10060

PRZYKŁAD

Obliczyć całkę

JJj(;c² + y²)dxdydz

v

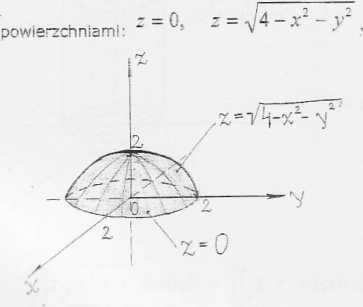
, gdzie V jest obszarem przestrzennym V ograniczonym

0 < ę < 2n

fJo<©<—

y

0 < r ^ 2

oraz x² +y² — r² cos² <psm² ® + r² sin² $>sin² © - r² sin²©

213    2    2

n

2U 2

jj{(>² + y²)dxdydz = Jc^Jr² sin²©-r² sin ©c?r = jd<p Jsin³®d@^r

0 0 0

o o

cos© = £ sin ®d® m -dt

O ©	X
	o

o o

32'.    .    ,

= — Jdq> J sin³© d® =

0    0 sm² ©-sin 0

-i -y 2n ]    ~ ~ 211

= ~ fd<p f(i-t²)dt = — j

dę

32

128.

■— i-- -2n=—-2n^—n

Cl    O I    i ^

15

■Zastosowania całki potrójnej w fizyce

Jeżeli przez P\^xiy>z) oznaczymy gęstość obszaru przestrzennego (funkcja ciągła w założeniu) to otrzymamy:

Masa V:

\M = JJjp(x, y, z)dxdydz v

4