83485 new 74

150 7. Zasady obliczeń wytrzymałościowych śrub

^d- = ^Qj£nn^^r-    ⁽⁷-⁶⁸⁾

gdzie Q jest obciążeniem, a i b — średnimi promieniami górnej i dolnej płaszczyzny przylegania pierścienia, r₀ — odległością środka ciężkości przekroju poprzecznego pierścienia od osi pierścienia, I_x — momentem bezwładności przekroju poprzecznego pierścienia względem osi x przechodzącej przez środek ciężkości przekroju i równoległej do podstawy pierścienia.

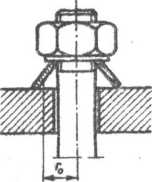
7.25. Zmniejszenie sztywności śruby przez zastosowanie podkładki sprężystej

Podatność w układzie szeregowym li = di/Q (śruba—pierścień) jest równa sumie podatności elementów składowych dJQ — ói/Q + Ś_spr/Q,

zatem sztywność śruby z elementem (elementami) sprężystymi Ci — Q d_t jest mniejsza niż sztywność śruby bez tych elementów.

Naprężenia zginające w pierścieniu wyznaczyć można ze wzoru

o_a =

Q(b-a)

h,

(7.69)

gdzie h jest wysokością pierścienia.

7.5.3. Określenie sztywności elementów łączonych

Określenie sztywności elementów łączonych w porównaniu z określeniem sztywności śruby jest zadaniem znacznie trudniejszym. Wynika to stąd, że trudne jest określenie przestrzeni, w jakiej zachodzi ściskanie. Poprawne określenie sztywności jest możliwe tylko na drodze pomiaru , odkształceń i obciążeń rzeczywistego układu. Nie można jednak wykorzystać tej metody w obliczeniach projektowych. W podręcznikach z Podstaw Konstrukcji Maszyn stosuje się zazwyczaj bardzo uproszczoną metodę obliczeń, w której przyjmuje się, że obciążoną objętość (w której zachodzą odkształcenia) wyznacza stożek ścięty z walcowym otworem (rys. 7.26). Średnicę mniejszej podstawy stożka przyjmuje się równą wymiarowi „pod klucz” a kąt pochylenia tworzącej stożka a —45°. Następnie w celu uproszczenia obliczeń stożek zastępuje się walcem drą-

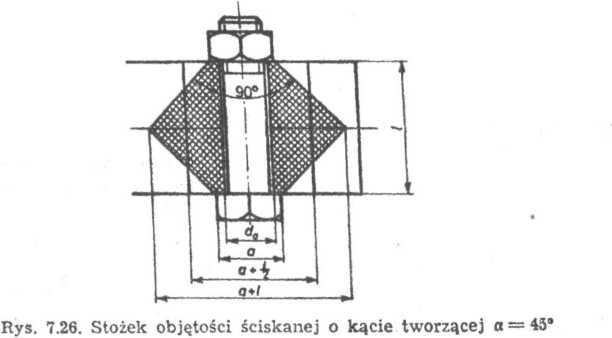
żonym o średnicy zewnętrznej a — równej średniej średnicy stożka.

Pole przekroju tego walca (rys. 7.26) jest równe F₂ = — [(a^-!^-    — d*j

i stąd sztywność elementów łączonych

^Ci i

Taka metoda obliczeń daje jednak bardzo niedokładne wyniki, szczególnie przy dużych grubościach łączonych elementów. Znacznie dokładniejsze wyniki można uzyskać drogą określenia odkształceń kołowosy-metrycznie obciążonej półprzestrzeni.

Przemieszczenia osiowe punktów okręgu o średnicy Oi (rys. 7.27) na podstawie [3] wyrażą się wzorem

₍₇₇₀₎

a

gdzie v jest współczynnikiem Poissana, p — ciśnieniem działającym na półprzestrzeń.

Uwzględniając, że odkształcenia obejmują objętość stożka, naprężenie ściskające a_t (przy założeniu jego równomiernego rozkładu) w dowolnym przekroju stożka jest równe

Q    -jp(^a* - °i)    ₍₇ 71)

°^z    jiz³ tg² a    jiz²tg²a    4z²tg²a

Przemieszczenie płaszczyzny półprzestrzeni dla z = b zgodnie z prawem Hooke’a określa wzór