str014

Wykazaliśmy zawieranie rolo C Win 1^H.

Jeżeli B € VJlr\2^u, to dla dowolnego AC H

»’o(A) = p*(A) = /x*(A n B)+ ii "(A - B) = pS(A n B) + pJ(A - B),

więc b e roi₀ i nn n 2* c roi₀.

13.    Zawierania nn₀ C M n2^a dowodzi się tak samo jak w zadaniu 12. Zauważmy, te H £ SI, natomiast H € EDlo, więc

roi₀ ± roi n2^w.

14.    Należy sprawdzić warunki a), b), c) z definicji 4. Mamy p"(0) = 0, ponieważ

r(0) = 0.

Niech AC B C X, dla dowolnego r > 0 istnieje ciąg zbiorów {A_n}_ngn, A_n £ V takL ie A C B c U^i-'⁴" > D“=i^r(-⁴n) < p*(B) + £• Oczywiście, p"(A) < H^-i^An)- Z dowolności liczby s > 0 wynika, że fi'{A) < fi’(B). Wykażemy,

^’(U”=i ^n) <    dowolnego e > 0 i dowolnego n £ K istnieje

fiąg zbiorów {A**}^,, taki, że A„ C UH=i ^Ank i

i    CO

i-=i    ¹

Stąd otrzymujemy Ur=i ^A" C U«i U^i -⁴«t >

<■•( U AOsEŚ^isiy wo+c.

y    n=l    n=lfc=l    n=l

Z dowolności t > 0 wynika, że

n‘(l)A_n)<jrii'(A_n).

n=1    n=l

15. Ze wzoru (*) z zadania 14 wynika, że dla dowolnego zbioru A £ V lĄ(A) < n(A)    i p*,(A) < ra(A).

Niech B będzie dowolnym podzbiorem przestrzeni X, a e dowolną liczbą dodatnią. Istnieje ciąg zbiorów {B_n}„_eu taki, że B_n £ V, B C Ur=i ' /'H-⁸) + £ > Cn=i ^ri(B_n)' Zachodzą następujące nierówności

'M    00    CO    CO

E^r^) >    = X>;(^B«) * /*;( U(^s^) >^(^B)-

n=l    n=l    n=l    n=l

Z powyższych nierówności i z dowolności f > 0 wynika, że it\(B) > n\[B). W analogiczny sposób otrzymujemy, że    > pJ(J3). Skąd wynika równość

ł»i = /i?.

16. Niech A będzie dowolnym podzbiorem zbioru X. Dla dowolnego n 6 N istnieje ciąg zbiorów {A_nk)jb€H taki. że A_nt £ V,

AC U Ant,    £t(Ank)</<’(A) + i.

k=l    fc=l

Niech A_n = U*Li Ant- Wtedy

M*(A„) < f]ś(A_nk) < f>(.4_nt) < /i*(A) + i.

Połóżmy B =    . wówczas A C B, więc fi'(B) > fi'(A). Z drugiej strony

fi‘(B) < ^'(An) < p"(A) + ^ dla dowolnego n £ N. Stąd otrzymujemy, że fi'{B) < /r*(A). A zatem zachodzi równość

fi-(B) = n-{A),

przy czym B 6 V,i.

17. Aby otrzymać miarę zewnętrzną fi" z zadania 7, należy rozważyć rodzinę V złożoną tylko ze zbioru pustego i przestrzeni X i położyć r(0) = 0, r(A) = 1.

Miarę zewnętrzną /i’ z zadania 8 otrzymujemy, rozważając rodzinę V złożoną ze wszystkich właściwych podzbiorów X. Funkcję r definiujemy następująco:

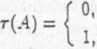
gdy A = 0,

gdy A/A', A CA.

Miarę zewnętrzną /i* z zadania 9 otrzymujemy, rozważając rodzinę V złożoną ze zbioru pustego, przestrzeni X i wszystkich zbiorów jednopunktowych. 'Natomiast funkcję r definiujemy następująco:

«-{5

gdy A ^ X, gdy A = X.

Miarę zewnętrzną p’ z zadania 10 otrzymujemy, rozważając rodzinę V złożoną ze zbioru pustego, przestrzeni X i wszystkich podzbiorów 1 kategorii przestrzeni X. Natomiast funkcję r definiujemy tak, jak w przypadku miary /r*, z zadania 9.

18. Nierówność (1) wynika z definicji fi‘ i własności kresu dolnego.

Aby zachodziła nierówność (2), wystarczy rozważyć rodzinę V złożoną ze wszystkich podzbiorów X i funkcję r zdefiniowaną następująco:

r(A)

gdy A* A, A CA, gdy A = A.

Wówczas na podstawie wzoru (*) z zadania 14 otrzymujemy, że fi*(A) = 0 dla dowolnego A C A. Zatem 0 = fi’(X) = r(A) = 1.