Strona0117

117

n

n

y* +    • ^sij⁺ lL^akh^sji =°

(5.32)

gdzie: ak - współczynnik tłumienia wiskotycznego.

Jeżeli każdy z kierunków k pokrywa się z każdym z kierunków j (tj. jeśli wszystkie elementy tarcia są przyłożone do mas układu), to liczba równań (5.32) jest równa rt. Jeżeli są także elementy tarcia, które dają siły oporu nieprzyłożone bezpośrednio do jednej z mas układu, to równanie (5.32) można ułożyć także dla kierunku działania tych sił, przy czym każdy z takich elementów tarcia zwiększa liczbę stopni swobody układu. Rozwiązanie układu równań (5.31) opisują drgania swobodne tłumione, tj. drgania, jakie wykonuje układ mechaniczny wyprowadzony z położenia równowagi, nadając mu warunki początkowe ruchu różne od zera. Warunki te zapisano w następujący sposób dla / ~ 0:

(5.33)

?/ = ?*> i =    0' = U2, ...,n)

Przy tych warunkach początkowych należy zbadać przebieg rozwiązań układu, np. (5.31). Tok postępowania jest następujący. Rozwiązania układu (5.31) szukamy w postaci funkcji:

(5.34)

qi = Ąe^At (i ~ 1, 2,..., ń)

gdzie: A_{ — pewne stałe rzeczywiste,

X - liczba rzeczywista lub zespolona.

Po podstawieniu (5.34) do (5.31) i uproszczeniu przez e^h otrzymamy

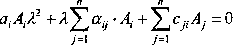
(5.35)

Jest to liniowy układ równań algebraicznych o niewiadomych A_t. Układ ten ma niezerowe rozwiązania, jeśli współczynnik przy niewiadomych jest równy zeru. Współczynnik ten piszemy w następującej postaci:

(5.36)

a_tA² + a_uA + c_u,c_in a_2iX.,a₂X + a₂₂A + c₂₂,c_2n

a„,A,a„A² +a„„A + c_im>c,

ni ’ n    tut tin? i