Wyklad (26)

(39)

x = Acos(cot -<p) mit tan (p —

2 po

2 2 co₀ -co

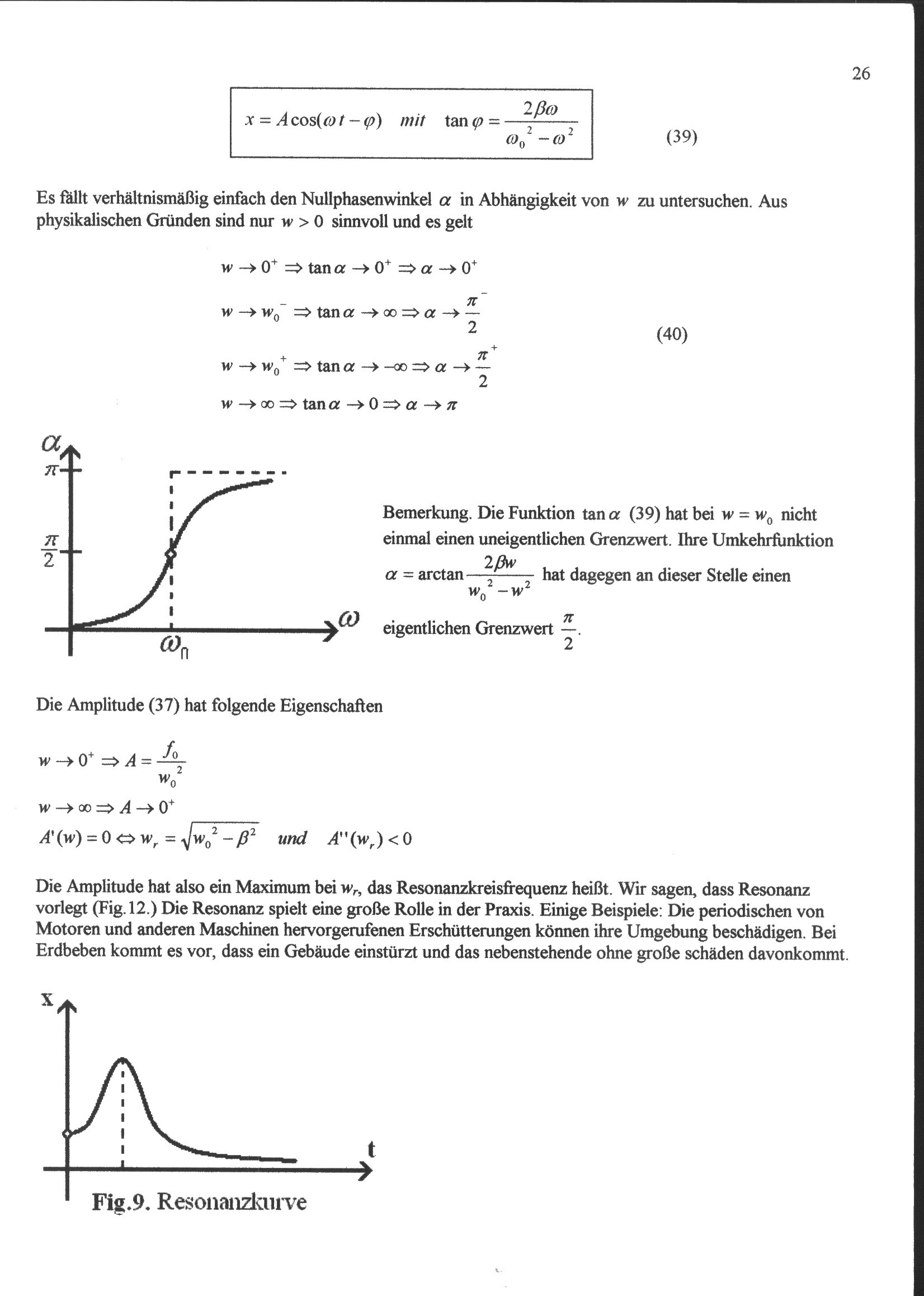
Es fallt verhaltnismaBig einfach den Nullphasenwinkel a in Abhangigkeit von w zu untersuchen. Aus physikalischen Griinden sind nur w > O sinnvoll und es gelt

w —» 0⁺ => tan a -> 0⁺ => a —> 0⁺

n~

w ->=> tana-^ooz>a->-

(40)

2

+    n

w ->w_a => tan a —» -oo => <2    —

2

w -> oo => tan a O => a 7r

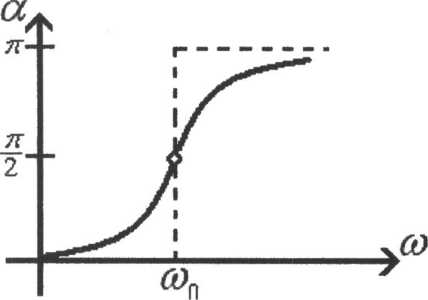
Bemerkung. Die Funktion tan a (39) hat bei w = w₀ nicht einmal einen uneigentlichen Grenzwert. Ihre Umkehrfunktion

a = arctan—— hat dagegen an dieser Stelle einen

w₀ -w

eigentlichen Grenzwert —.

Die Amplitudę (37) hat folgende Eigenschaften w -» O^ł => A = -Ą-w -» oo => A -» 0⁺

A'{w) = O <=> w_r = ^/w₀² -p² und v4^M(w_r)<0

Die Amplitudę hat also ein Maximum bei w_r, das Resonanzkreisfreąuenz heiBt. Wir sagen, dass Resonanz vorlegt (Fig. 12.) Die Resonanz spielt eine groBe Rolle in der Praxis. Einige Beispiele: Die periodischen von Motoren und anderen Maschinen hervorgerufenen Erschutterungen kónnen ihre Umgebung beschadigen. Bei Erdbeben kommt es vor, dass ein Geb&ude einstiirzt und das nebenstehende ohne groBe schaden davonkommt.

X

Fig.9. Resonanzknrve

t