003 8

9.5. PROSTE STYCZNE DO DWÓCH DANYCH OKRĘGÓW

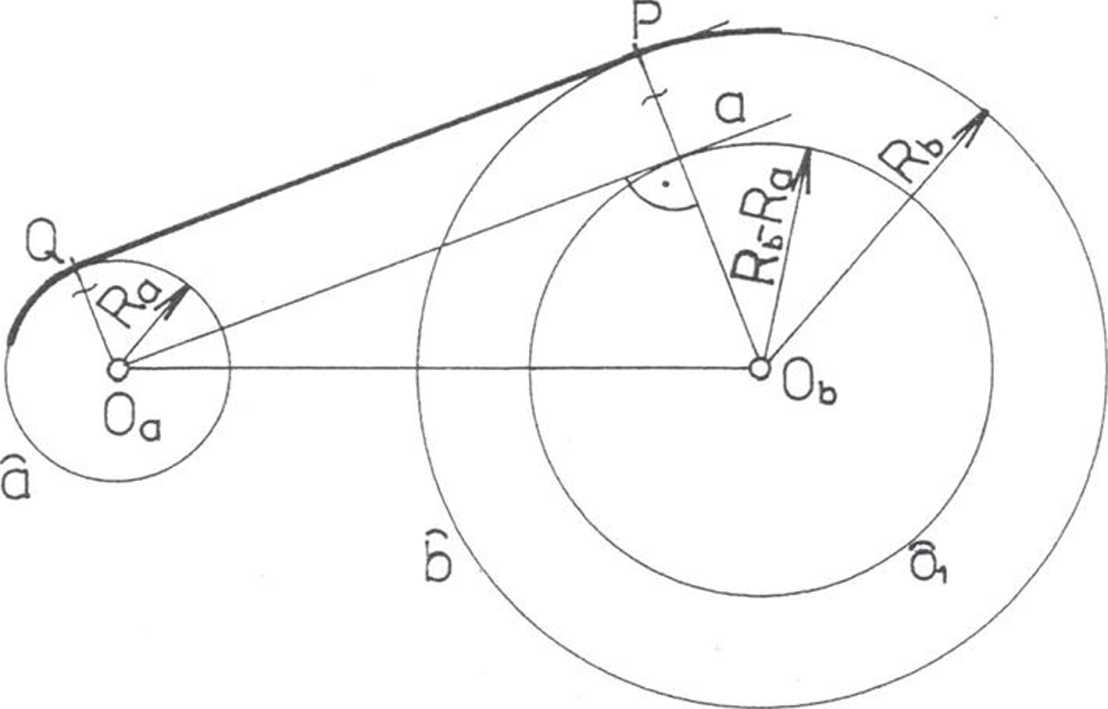
Do dwóch danych okręgów a i b można poprowadzić cztery proste styczne, które można określić jako zewnętrzne lub wewnętrzne.

Aby wyznaczyć proste styczne zewnętrzne, przeprowadźmy następujące rozumowanie. Gdybyśmy poprowadzili prostą przechodzącą przez punkt O_a, równoległą do szukanej stycznej, byłaby ona styczna do okręgu d₁ o środku O_b i promieniu równym różnicy promieni R_b — R_a.

Wobec tego, aby wyznaczyć prostą styczną zewnętrznie, należy kolejno:

-    narysować okrąg o, o środku O_b i promieniu P₇ = R_b — R_a,

-    narysować prostą a styczną do okręgu o, przechodzącą przez punkt O_a,

-    wyznaczyć punkt P, w którym prosta, przechodząca przez punkt O_b i prostopadła do prostej a, przecina okrąg b,

-    przez punkt O, poprowadzić prostą równoległą do promienia O_bP, która przetnie okrąg a w punkcie Q.

Prosta przechodząca przez punkty PO jest szukaną styczną zewnętrznie, a punkty P i 0 są punktami styczności

c

V

Aby wyznaczyć styczną wewnętrzną, przeprowadzimy podobne rozumowanie. Prosta równoległa do szukanej stycznej poprowadzona z punktu O_a

jest styczna do okręgu o₂ o środku w punkcie O_b i promieniu P₂ = P_a + R_b. R Aby wyznaczyć prostą styczną wewnętrznie, należy kolejno:    o

-    narysować okrąg o₂ o środku O_b i promieniu P₂ = R_a + P_b,    z\

- wyznaczyć prostą b styczną do okręgu o₂, przechodzącą przez punkt O_a,    ki

- wyznaczyć punkt P, w którym prosta, przechodząca przez punkt O_b    łą

i prostopadła do prostej b, przecina okrąg b,    k<

54

i