3110398547

Rozwiązanie. Niech O będzie środkiem rozważanego okręgu stycznego do trzech danych okręgów i niech S będzie punktem styczności tego okręgu z okręgiem o środku A (zob. rysunek):

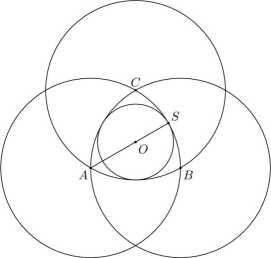
Oczywiście punkt O jest środkiem ciężkości trójkąta ABC oraz punkty A, O i S są współliniowe. Mamy wówczas

OS = AS-AO = 2 - | -    = |. (3 — V3).

19. Dany jest odcinek AB o długości 2. Punkty A i B są środkami okręgów o promieniu 2. Udowodnij, że okrąg styczny do prostej AB, styczny zewnętrznie do okręgu o środku A oraz styczny wewnętrznie do okręgu o środku B (zob. rysunek), ma

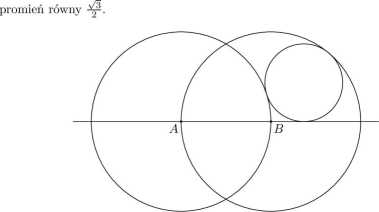
17