0000088

10.2.1. Algorytm wyznoczonlo dondrytu dróg najdłuższych

O o n c x Siać cklorowann boz dróg cyklicznych o pootocl S - <G.f>. (l\> . C - <X.r> , r«X— 2^xł 1 »    ; u.

• {<x.y> * (x,y,£X) A (y € Tx)J ; x^p - wierzchołek poczętko-wy (korzoń dondrytu).

Procedura t

1° i'«yznaczony warstwy digrofu C : ^x0^xi‘»••***• Oznaczmy przoz 1 numer worotwy, do której należy wierzchołek x^p ; *^p£Xj,

K - oznacza numor ostatniej warstwy.

2° Będziemy cechowali wierzchołki x€X cechami podwójnymi

(F(x), y(x)). W tym colu przez C oznaczymy zbiór wierzchołków. które so aktualnie ocechowane. Zadanemu wierzchołkowi , x^p nadajemy cechę (0.0), to znaczy F(x^p) • 0. y(x^p) ■ 0.

W tej chwili C • {x^pJ. Podstawiamy i i ■ 1 ♦ 1.

3° Pytamy czy i > K ?

NIE: Bierzemy pod uwagę warstwę (nostępnę w kolejnoócl).

Bierzemy pod uwagę wierzchołki xCX₁ takie, dla których zbiór ocechowanych poprzedników nie Jeot pusty. P “^l( x )ACjfp. Olo kożdego wierzchołko xCX., którego zbiór ocechowanych poprzedników nie jeot pusty, obliczamy wartość lewej ce -chy

F(x) ■ *ax [l(y .x) ♦ F(y)] yer^jnC

Ooko wartość prowej cechy y(x) wierzchołka x przyjmujemy ten wierzchołek y, przy którym powyższe wyrażenie przy -jęło wartość ckotremolnę.

C i • C k/ (x).

Po rozpatrzeniu wozystkich wierzchołków xCpodstawiamy i i • i * 1    1 przechodzimy do punktu 3°.

TAK t Przochodzimy do punktu 4° (rozpatrzone zostały wszystkie warstwy).

4° Zbiór ocechowanych wierzchołków C Jeot zbiorem wierzchołków oslęgalnych z wierzchołka x^p. to znaczy stanowi zbiór wierzchołków noksymalnego dondrytu najdłuższych dróg. od wierzchołka x^p, w sieci S.

Oługoóc najdłużeżoj drogi z x^p do dowolnego wierzchołka xCC określona Jeot wartoócię lewoj cochy F(x) togo wierzchołka. Drogę ty wyznaczają prawo cechy wierzchołków poczy-najoc od wiorzchołka x^k i przoeuwajęc oiy do wierzchołka x^p przeciwnie do zwrotu łuków (od koóca). Znojdujęc w ten epoaób ontydrogi do wierzchołka x^p. dla każdego wierzchołka x£ C, wyznaczamy w eieci 6 cały dendryt rokoymolny najdłuższych dróg, od zadanego wierzchołko x^p. Praktycznie, noloży do każdego wierzchołka x doprowadzić Jader łuk od wiorzchołko okreólonogo wartości* prawej cechy y(x).

Przykład 10.2

Bioręc Biec S z przykładu 10.1, przedatowion* w układzie warstwowym na ryą.10.4, etosujemy algorytm pkt 10.2.1, przy założeniu x^p • x₀. Oako łuk <x₇,x₄> przyjmujemy, zgodnio z uwo-go 1, łuk Ujj. Otrzymujemy zbiór ocechowanych wierzchołków C •

" {^x2'^X3'^X4'^X5'^X6'^X7'^x8'*9 ) * ^0trzy^mono cechy przodotawia tablica 10.7.

• Tablica 10.7

X	^X2	^X3	^X4..	*5	^X6	^x7	^X8	^X9
F( x)	26	27	38 .	34	24	11	0	8
y(*)	^X6	^X2	^X7	^X6	^X7	^X9	9	^X8

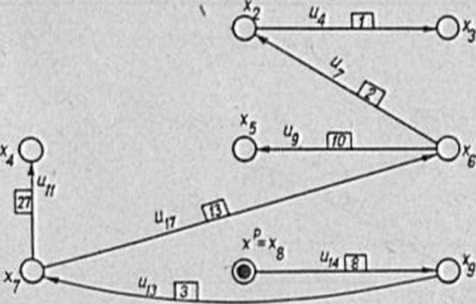
Rye.10.5