0000097

Zadanie komiwojażera nota być aformułowane jako zadania programowania binarnego. W szczególności sformułowanie to noże przyjąć naetępojęca postać [22]

X • fx I    ; i.j ■ 0.1.2.....n jaat macierz*

L ^XJJ(n*l)a(nalJ

zmiennych binarnych

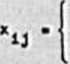
1 gdy komiwojażer jadzie z miasta 1 do J

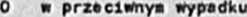
Naloty wyznaczyć tak# macierz X^#. aby

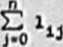
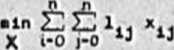
przy ograniczeniach

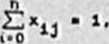
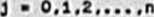
5Ż^xij ■ 1.    1 • 0,1,2.....n

u₁ - Uj ♦ nx_1J « o-l. i.J ■ 0,1,2,...,nj i / j gdzia u_A a« zaiannyai przyjmującymi dowolna wartości rzeczywista. Sforaułowana zadania można rozwiązać metodami programowania eał-kowitoliczbowego. Naloty jadnak zwrócić uwag*, to Jut nawet dla nlawialkisj wartości n (na przykład SO) ilość zaionnych. która muszą występować w zadaniu, jaat olbrzymia (2652). Widać zatoa wyróżnia praktyczno nieprzydatność aatod programowania aateaa-tycznago dla rozwiozywanla togo typu zadań.

Oute znaczania praktyczna zadania koalwojatara Wynika z togo, te wiele zagadnień z teorii organizacji oprowadza sio właśnie do takiego zadania (na przykład problem wyznaczania kolejności operacji przy realizacji danego przedsięwzięcia). Zadanie powytsze nie doczekało alf dotychczas efektywnej, ogólnej metody rozwiązania.

Rozdział 11

PRZEPŁYW MAKSYMALNY

Problem wyznaczania przepływu maksymalnego występuje przy planowaniu transportu w sieci dróg (rurocięgów) o ograniczonej przepustowoócl [l4] , [10] . Modelom takiej elecl nota być eleć formalno S ■ <G,{o},{h}> , gdzie 0 - <X,U,P> jeot opójnym grafem Oerge'0 bez pętli, a(x) Jeet funkcję określono na zbiorze wierzchołków xCX, wyrótnlejęcę w sieci dwa wierzchołki! s -- źródło oraz t - odpływ

1	dla	X •	s
0	dla	* /	• ,t	•
. -1	dla	X ■	T

natomiast h(x,y), jaat nloujemnę funkcję na zbiorze łuków <x,y>6U digrafu C, 04 h(x,y)<oo , któraj wartości sę Inter -pretowane jako przepustowości poszczególnych łuków aiecJ. »ieó S będziemy nozywali standardowo eleelę t ransportowę. Oażell S jeet modelem elecl wodoclę-gowej, to wartość h(x,y) lnterpretujo się jako makeymalnę, dopuszczalno ze względu na ciśnienia. Intensywność przepływu wody przez odcinek rury reprezentowany łuklem <x,y> .

Przepływem w elecl S nozywamy dowolnę funkcję f 1 U —R epełniajęcę naetępujęce dwa warunki

1/

04f(x,y)4 h(x,y)

2/

A

*ex

2HT f (x,y)

yerv)'

■ »(*) v(f)

2«P‘V)

gdzie P(x) jest zbiorem następników wierzchołka x, a P"¹(x)

i9ir