0000126

wraz z woktoroa Jodynkovrym przedział A( ⁿ ^, 1 ), na którym f ul. Utwórzmy teroz iloczyn logiczny tych zmiennych boolonakich,któro odpowiadaję Jodynkowym okładowym woktora X'ⁿ). Łotwo zauważyć,

Ze iloczyn ton bodzie miał wortodć i dlo wszyotklch woktorów z przedziału A(j^ⁿ^, f ), a worfodć O pozo tym przodziałom. Podobne iloczyny utworzymy dlo wozyotklch woktorów zbioru X[ⁿ^, o nootępnie troktujęc Jo jako okłodniki, utworzymy ounę logiczny tych akłodnlków. Otrzymono rryroźonio oltornatywno-koniunkcyjno okredle funkcję f. Zetom, dlo każdej funkcji eonotonicznej iot-nioje wyrożenio oltornatywno-koniunkcyjno utworzono w powyżuzy eposób. Nosi ono nazwę połnoj form-uły alternatywno j (pfo).

Wykożony teraz, że Jożell wyrażenie okrodlajęco funkcję f Jest wyroźoniem oltornatywno-koniunkcyjnyo, to f Joot funkcję ronotonicznę. Załóżmy w tym colu, że powyżozo tezo Joot nie -prowdzlwo, to znaczy istnieję dwa woktory X^ⁿ^x^ⁿ) oraz f(x<ⁿ>) -li f(xjⁿ)) ■ 0. Przokertołcimy wyrażenie okrodle-jęco funkcję do pootoci oumoiloczynu logicznogo. Po podatowio-niu wektora xj°) wartość tego wyrożenio będzie równo 1, to znaczy przynajmniej Jedoń z iloczynów (okłodnlków oumy) będzie miał wortodć 1. Weźmy pod uwegę ten iloczyn. Dlo wszyotklch woktorów, które sę naotępniknmi woktora X^ⁿ), wortodć teoo iloczynu muoi pozootać równo l, a więc i dlo woktoro otrzymamy wortodć całego wyrażenia równg 1. Otrzymalldmy oprzecz-noóć z założeniem, źo f(x^) ■ 0, któro kończy dowód twierdze-nlo 0.1.1.

Dlo funkcji monotonicznoj dofiniuje oię pojęcie tok zwo -nych woktorów minimalnych. W a k t c ram minimalnym funkcji monotonicznoj f(x^ⁿ^) nazywa oię każdy taki wektor    , że f(*^^    ■ 1, ą dla wozyotklch woktorów x(ⁿ ^

taITIćh7~ie~X_i^ⁿ^H'    ~1    f( )~Ó. Zbiór

weFtorów niiniinolnvc~?unkc1l monotonicznoj oznaczymy prze z ^“min * ^Foroolny    definicji Jeet neotępujęcy

[,(">. X^)]«['(_x^(n,j. i]a[ A    <">>*#> * *⁽ⁿ⁾)-

-ó-CH^xiⁿ⁾) • °)]    (D.i.ie)

o tanowi! drio woktory <0,1,0,0> l <1,0,1,0) , oznoczonc no ryo.D.1.2 zo pomocę .

Z definicji funkcji monotonicznoj 1 woktoro mlnimolnogo

okroólo w opooób Jodnoznaczny funkcję blór    Joot eumę mnogoóciowę przo-

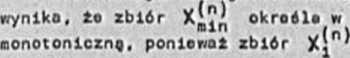
działów, w których woktoroml najoniejezyni oq woktory minimał-no, a woktoroa nejwlękezym - woktor o wozyotklch okładowych Jo-dynkowych (woktor jedynkowy). Z tym oototnln wniookion wlężo oię pojęci© tok zwanoj mininolnoj formuły oltornatywnoj (mfo), okreólojęcoj monotonicznę funkcję boolowokę.

Minlmalnę formułę alternatywno funkcji boolowokloj nozywamy wyrażonio boolowoklo okroólojęco tę funkcję, o pootaci oumolloczynu logicznego, zowiorojęco noj-mniojozę iloóć okładników ouny (nioredukowalne). No mocy twior-dzenlo 0,1.1, kożdę funkcję nonotonicznę możemy przodatawić za po.-aocę mininolnoj formuły altcrnotywnoj. No przykład, wyrożenio (0.1.14) możno przokoztołcić (zrodukowoć) do pootoci mfo w no-etępujęcy epooób

(x_Av x₂)a(x₂vx₃)v (x₁ax₃ax₄) .

■ x₂v (x₄a x₃) V (XjA x₃ ax₄) • X₂v(XjAX₃)

Zatem funkcjo, ołużęca jako przykład w punkcie 0.1.2, możo być przodstowiona zo poiaocę mfo naetępujęco

f (x^l) ■ x₂ v (x_x ax₃)

Widać toroz wyrożnio, żo nie zależy ona od zmiennej x₄. Przy -pomnijmy, żo woktoroml minimalnymi tej funkcji eę woktory <0,l,0,0> i <1,0,1,0> oroz porównajmy te woktory alnlmalne ze ekłednlkaai oumy logicznoj mfo. Widać wyraźnie odpowiednioóć między woktoroml minimalnymi i odpowiodnimi iloczynomi (okłod-nikomi oumy) wyetępujęcymi w mfa.

251*