047(1)

Zastępując ~ przez 7 (,v, y) możemy wyrazić drugą pochodną tylko przez ,v i y

f/¹y

v,7i(x,y)] =y(x,y)

Zupełnie tak.samo można wyrazić tylko przez „v i y pochodne funkcji uwikłanej wyższych rzędów, trzeba tylko za każdym razem, gdy przy różniczkowaniu wystąpi pochodna ^, zastąpić ją funkcją 7 (x, y)r

Do tego samego wyniku dojdziemy także różniczkując kolejno równość f(x,y) — 0, a następnie eliminując z otrzymanego układu równań wszystkie pochodne rzędu niższego.

226. Wyznaczyć pochodne następujących funkcji uwikłanych:

^wyz°^aczy4S

2) e'^p~¹-\-r(f~3r—2 = 0; obliczyć ^ dla cp = 2

3) x» = y*j

, dx

wyznaczyć

4)    ar-J-y¹—4jc—lOy i-4 = 0; obliczyć y' dla x = 6. Jaki sens geometryczny ma rozwiązanie tego zadania.

5)    t—s+arc tg s = 0; wyznaczyć s"

6)    y = jc+lny; wyznaczyć y" oraz x"

Rozwiązanie: 1) Różniczkując względem x obie strony równania, w którym y jest funkcją x, otrzymujemy

2x _ 2yy'_ __ a¹ b¹~

Stąd znajdujemy

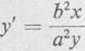
Z równania tego wyznaczamy

dr _ e*-²+r d<p 3—tp

Podstawiając daną wartość <p — 2 do wyjściowego równania, obliczamy odpowiadającą jej wartość r; mamy r,_P=2 = — 1. Zatem szukana wartość

pochodnej ~^r- dla <p = 2 (i r — — 1) będzie równa

= 0

/ dr \ e° — 1

3) Logarytmujemy (przy podstawie e) obydwie strony danego równania, a następnie różniczkujemy je względem y, traktując a: jako funkcję y;

otrzymujemy

y lnx = alny,    y' In A-f-y (In a)' = x'lny+A (lny)'

1 • ln A+y — = a' ln y+A —

a    y

skąd znajdujemy

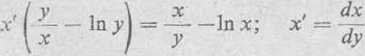
a (a—yln a) y(y—a ln y)

4) Różniczkując względem a, otrzymujemy

2A+2yy'-4-10y' = 0

stąd

/ =

a—2 5-y

Podstawiając daną wartość a = 6 do równania wyjściowego znajdujemy na y dwie wartości: y\ — 2, y₂ — 8. Wobec tego także pochodna y' przybiera dwie wnrtości dla a =' 6

4    4

y_x=6 = -3-. gdy y = 2; yU« = — -y> gdy y = 8

W układzie współrzędnych prostokątnych równanie wyjściowe przedstawia okręg, którego dwa punkty mają odciętą a = 6; są to punkty ²

97

1

Różniczkując dane równanie względem rp i traktując r jako funkcję q>, znajdujemy

2

MetoJy rozwiązywania zadań