087 4

Ponadto dolną graniczną wartość współczynnika przesunięcia xj można wyliczyć ze wzoru

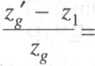
14-9

17

0,2941,

zaś górną graniczną wartość współczynnika przesunięcia x' przyjmuje się Xg < y, w naszym przypadku dla z - 9; Xg < 0,69 (rys. 13.2). Należy przyjąć wartość jcj z przedziału xj <    < x ', obliczyć wartość

przesunięcia X_l=x_lm, i o tę wartość należy odsunąć zębatkę od koła z,, czyli od położenia, które zajmowała przy zębach zerowych.

Sposób wykonania ćwiczenia dla koła o liczbie zębów Z\= 9:

a)    obliczyć średnice i narysować koła: podziałowe, stóp i wierzchołków zębów na uprzednio przygotowanym krążku papieru;

b)    zamocować na kole (2) uprzednio przygotowany krążek papieru;

c)    przesunąć zębatkę (3) o wartość X, =x, • m, zwiększając odległość zębatki od osi koła;

d)    obrysować zęby zębatki w kilku kolejnych położeniach koła (2) otrzymując zarys zęba bez podcięcia u podstawy, ale o zaostrzonym wierzchołku.

Według [10], grubość zębów mierzona na kole wierzchołkowym nie powinna być mniejsza od 0,25 modułu dla kół stalowych, zaś 0,4 modułu dla kół żeliwnych, by nie następowało wykruszanie się zęba.

Rysowanie uzębienia korygowanego gdy z₂ > z'.

Dane koła: m- 14 mm, y = 1, X₂ = x₂m, z₂ = 30, a_Q = 20°.

Zakładamy, że koło o liczbie zębów z₂ = 30 będzie współpracować z korygowanym kołem o liczbie zębów Z\ - 9.

Jeżeli przyjmie się z wykresu (rys. 13.2) dla z₂- 30, wartość współczynnika przesunięcia x₂ z przedziału B, x’_d < x₂< x' i o wartość przesunięcia zarysu X₂ = x₂m dosunie się do koła (2) zębatkę (3), zmniejszając odległość jej od osi koła, uzyskuje się w przypadku x₂ * —x_x korekcję zazębienia P, czyli korekcję powodującą zmianę odległości osi kół współpracujących.

87