100d28

Wskaźnikowanie dyfraktogramów na przykładzie dyfraktogramów substancji regularnych

Metoda różnic

h² +k^ł + l*

4 sin²0 ■ X²    '

|

1

$in^z0 ■ -( h² +k² +1³)

4 a²

X^ł/4a² = A, h²+k² + l^J = N sin²0| = AN|

sin²0»i - sin²0| = A(N*i - N|)

A_mi_n = sin^J0t*i-sin^J0, sin²©!

N,«-

A

Natężenie refleksu dyfrakcyjnego

Jhu = C- lF_hUl²-LP*p-A

/F_hU/² - czynnik struktury,

N - liczba komórek elementarnych w 1 cm¹

LP - czynnik Lorentza i polaryzacji (czynnik kątowy);

p - czynnik krotności płaszczyzn;

A - absorbeja;

Mo e^{2 2}

C = Jo *X.^J N¹ • -

4x mr

J₀ - natężenie promieniowania padającego;

X - długość fali;

Mo — przenikalność magnetyczna próżni;

e - ładunek elektronu;

m - masa elektronu;

r - odległość elektronu od punktu pomiarowego,

N - liczba komórek elementarnych w I cm.

Amplituda struktury Fhu

F_hU= £ f.eipfltFa)

n-l

f„ - atomowy czynnik rozpraszania n>tego atomu w komórce elementarnej;

t|/_B- kąt fazowy promieniowania rozproszonego na n-tym atomie w odniesieniu do promieniowania ugiętego na atomie położonym w początku układu;

V, = 2n(hx_n + ky. + Iz.)

N

Ffcu = 2 f. exp |2x i (hx. + ky. +

n^-l

Czynnik struktury |Fsu|²

I Fhu I ^J= |I f. cos 2x(hx, + ky, + lz.)|² +1£ f, sin 2x(hx„ + ky, + Izn)]²

Czynnik struktury |Fbu|² to zawsze dodatnia liczba rzeczywista

Amplituda struktury Fhu dla struktur

posiadających środek symetrii: N

Ft,u- £ f* cos2x(hx„ + ky„ +

w n=l

Amplituda struktury w sieciach typu I i F

Komórka przestrzennie centrowana I:

Fuj = f„ cos 2k (h-0 + k-0 + I-O) + f, cos 2x (h-V£ + k-*A + 1-'A)

Fm - 2 f.    dla h + k +1 = 2n)

Fuj = 0    dla h + k +1 = 2n +

1

Komórka płasko centrowana F:

Fuj = f, cos 2x (h-0 + k-0 + I-O) + f. cos 2x (h-J4 + k*'/i +1-0)

+ f_n cos 2x (h-'/i + k-0 +1-0) + f, cos 2x (h-0 + k-'/i + I-O)

Fuj-4f. dla h + k +1 = 2n

Fhu “ 0 dla hkl mieszanych (np. 223, 230 itp.)

Obliczenia parametrów komórki elementarnej oraz jej objętości

• w oparciu o dane, wykorzystane do wskaźnikowania:

a.- V X*/4A luba.- | 1/ B

•••■dsu V Ni

• wykorzystując funkcje ekstrapolacyjne np.

Ad/d - f(Kcos^,0)

(dla 0 powyżej 60*), dla której otrzymuje się wykres a₀ ■ f(cos²0)

Ekstrapolując dla 0 ■ 90°

(cos²0 - 0) wyznacza się wartość a₀

Objętość komórki elementarnej

>' - aSr^l • oa*‘ a - eo*¹ fi - ca.' yl eow ootfimj

Gęstość rcntgcnograficzna (teoretyczna)

masa komórki: M = p V p -gęstość piknometryczna

V - objętość komórki

Liczba cząsteczek (atomów, jonów) w komórce elementarnej:

pV

Z* - m-

rzeczywista masa cząsteczki (atomu, jonu)

m

Gęstość rentgenograficzna:

A-Z

p_r--1.6602 • 10'²⁴ [g/cm³|

V

A- ciężar cząsteczkowy

Obliczanie wielkości krystalitów

Ze względu na wpływ wielkości krystalitów na wygląd

dyfraktogramu, można ich rozmary uporządkować w trzy zbiory:

•    krystality większe niż lOpra;

•    krystality, o wymiarach w granicach od 0,1 pm do 10pm;

• krystality mniejsze od 0.lpm..

K X

p_t - ......wzór

Scherrera

Dui cosOuj

Pt - szerokość refleksu,

K - stała Scherrera, (bliska jedności),

Dtu - średni wymiar krystalitu w kierunku prostopadłym

do plas/r/y/Jt B

0uj r kąt odbłysku dla refleksu bkJ.

Metoda Halla wyznaczania wielkości krystalitów

ki

Badanie tekstury

Tekstura: występowanie w próbce uprzywilejowanego kierunku (tekstura włóknista) lub płaszczyzny w ilości przekraczającej statystyczne nieuporządkowanie.

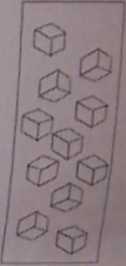
kierunek [001]

łlłwczyzw (001)

to oznaczone alfabetycznie literami pozycje atomów (jonów) w komórce elementarnej o lokalnej symetrii punktowej stanowiącej podgrupę sy metrii przestrzennej kryształu.