10 (55)

Rozdział 10

Całkowanie form zewnętrznych

Całkowanie może być rozpatrywane na wielu poziomach. W rozdziale 6 teorię taką rozwinęliśmy dla dostatecznie porządnych funkcji określonych na podprzedziałach prostęfj rzeczywistej. W rozdziale 11 poznamy znacznie bogatszą teorięćałko wania, mającą zastosof wanie do znacznie szerszej klasy funkcji, które mogą być określone na niemal dowolnych! podzbiorach R". Obecny rozdział traktuje o tych aspektach całkowania, które pozostają w ścisłym związku z geometrią przestrzeni euklidesowej. W szczególności zajmiemy się takimi zagadnieniami jak formuła zamiany zmiennych, całki krzywoliniowe i machina zewnętrznych form różniczkowych umożliwiająca sformułowanie i udowodnienie n-wymiaroj wego analogonu podstawowego twierdzenia rachunku różniczkowego, a mianowicie twieiM dzenia Stokesa.

Całkowanie

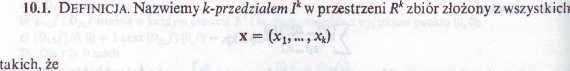
a_f ^Xi<bt U = 1,..., k).

0)

Niech P oznacza /-przedział w zdefiniowany przez pierwszych / nierówności (lj* a/** funkcję rzeczywistą ciągłą na /*.

Niech/=f_k i zdefiniujmy funkcję/* _ j na l^k~¹ wzorem

/__x(x₁₉    , x_k-_u x_k)dx_k.

Z jednostajnej ciągłości/* na 1* wynika, że/*_ _t jest ciągła na l^k~K Możemy zatem powtórzyć to postępowanie i otrzymać funkcje/-, ciągłe na V i takie, że/_ * jest całką z/ względem Xj na przedziale <flf, bj>. Po k krokach dochodzimy do liczby f₀, którą nazywamy całką zf na I^k. Zapisujemy to następująco:

[Mdx lub jf r *    W

(2)