123(1)

616.    Parabolą y = x^t+4x i prostą y+4 = 0

a I -    —^x\

617.    Linią łańcuchową y = \e^a +e °/ i prostymi .v = 0, x — a

618.    Hiperbolą xy = 6 i prostą y = l—x

619.    Parabolą sześcienną y = x³ i prostymi y — x, y — 2x

620.    Okręgiem x~^Jry¹ — 4x i parabolą y¹ = 2x

621.    Lemniskatą o² — a²cos 2<p

67,2. Pierwszym zwojem spirali Archimedcsa q = acp i osią biegunową

623.    Rozetą trójl istną o = «cos3ę;

624.    Kardioidą q — c(l—cosip) i okręgiem q — a

625*. Elipsami ~= 1 i    == 1

§ 4. Wyznaczanie objętości bryły na podstawie znajomości pól przekrojów

równoległych

Gdy znane jest pole S(x) dowolnego przekroju danej bryły' płaszczyzną równoległą do pewnej płaszczyzny P, gdzie x oznacza odległość płaszczyzny tnącej od płaszczyzny P (rys. 102), to przy zmianie x o wielkość dx różniczką

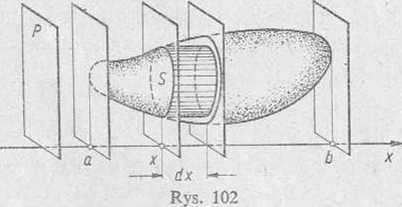
objętości będzie objętość walca prostego o wysokości dx i o polu podstawy S(x), czyli dV = S(x)dx, a objętość bryły wyrazi się całką

b

V = j S(x)dx    (*)

a

przy czym a i b stanowią odpowiednio lewą i prawą granicę przedziału zmienności x.    -

626. Obliczyć objętość części walca, odciętej płaszczyzną przechodzącą przez średnicę 2R jego podstawy i nachyloną do podstawy pod kątem a.

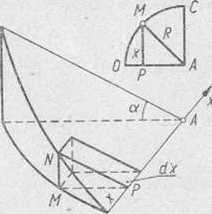
Roz w i ą z a n i e. Rysujemy połowę danej bryły (rys. 103) i stwierdzamy, że każdy z przekrojów' równoległych do płaszczyzny ABC jest trójkątem prostokątnym.

Obliczmy pole przekroju odległego o x od punktu O; x = OP. Z trójkąta prostokątnego AMP mamy MP¹ = R²—(R—x)², a z trójkąta prostokątnego PNM wynika, że MN = MPtga.

B

C

0

Rys. 103

Pole przekroju S(x), jako pole trójkąta prostokątnego o przyprosto-kątnych MP i MN, wynosi

S (x) = -- MP MN = y MPhg a =

= y [R²-(R-x)²] tg a = y (2Rx-x^t) tg «

Zmianie x o wielkość dx odpowiada zmiana A V objętości V, równoważna objętości prostego walca (tu graniastosłupa) o wysokości dx i o polu podstawmy S{x)

Całą szukaną objętość wyczerpiemy, gdy x będzie przebiegać od 0 do 2R, zatem

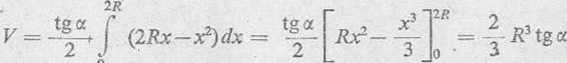
0

X⁴" y 2r

627. Obliczyć objętość elipsoidy trójosiowej y -j-y “r y = 1.

249