142 4

284

a)    b)

x3x, ^xl^x2\					I^X3^X4	1	1	0	1
	1 00	01	11	10	\^X3^X4 ^X1^XK	00	01	11	10
00	0	0	1	0	00	0	0	1	0
01	1	1	0	1	01	1	1	0	1
11	0	0	0	0	11	0	0	0	0
10	1	1	1	1	10	1	1	1	1

y    y

c) _ d)

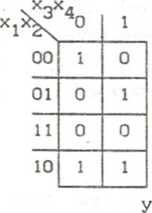
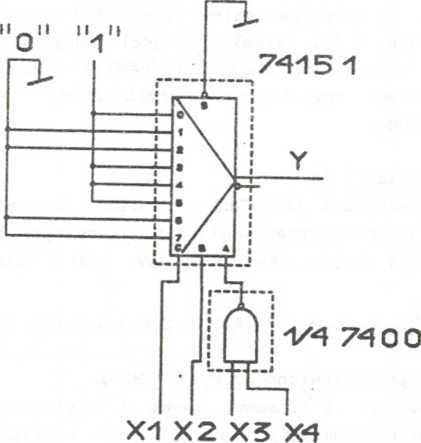
F-ys. 3.81. Realizacja funkcji z przykładu 3.44 z wykorzystaniem wejć adresowych multipleksera: a) tabela Karnaugha, b),c) tabel

jej równoważne, d) schemat

kierowane na wejścia układu będą występowały mniej razy niż w innych rozwiązaniach [8].

W sytuacji, gdy zachodzi potrzeba stosowania multiplekserów o liczbie wejść adresowych większej niż mają multipleksery produkowane, bądź aktualnie przez nas posiadane (r=l,2,3,4), należy dokonać łączenia multiplekserów o mniejszych wymiarach w multipleksery o większych wymiarach. Przykład układu wielopoziomowego przedstawiono na rys. 3.82 a (patrz również rozdz. 2.5.1, rys. 2.40). Na rys. 3.82 b,c przedstawiono ogólną zasadę powiększania wymiaru multipleksera, tzn. uzyskiwania multipleksera o (k+1) wejściach adresowych, gdy dysponujemy multiplekserem o k wejściach adresowych. Jeśli zachodzi potrzeba powiększenia liczby wejść adresowych do (k+2), to w stosunku do multipleksera (k+1) wejściach adresowych nr.leży jeszcze raz zastosować przedstawioną zasadę itd. W realizacji z rys. 3.82 b wykorzystuje się wejścia strobujące multiplekserów, zaś w realizacji z rys. 3.82 c niezbędne są dodatkowo multipleksery mające wyjścia typu otwarty kolektor (rozdz. 2.3).

a)    b)

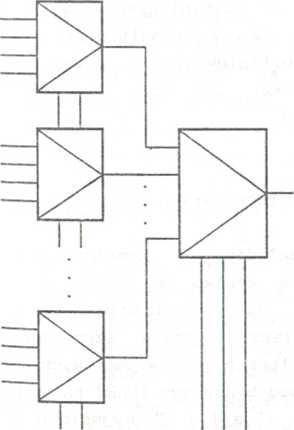
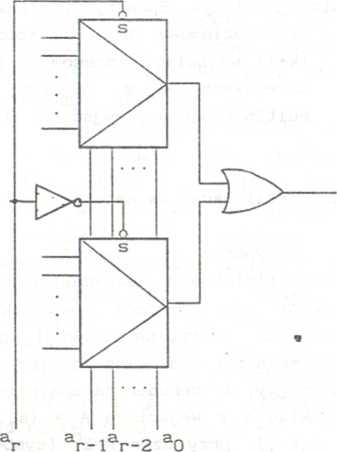
Rys. 3.82. Patrz ciąg dalszy