1tom214

430

8. AUTOMATYKA I ROBOTYKA

Jeżeli regulator diagonalny nie zapewnia dostatecznej jakości regulacji, to nal • zastosować regulator niediagonalny, ale taki, przy którym układ zamknięty jest odnrz nięty, tzn. dający URA, w którym transmitancja układu otwartego jest diaeona. Projektowanie regulatora odprzęgającego jest proste w przypadku minimalnofazow^ obiektu regulacji. Regulator w takim przypadku składa się z 2 części: diaeonafn^ i niediagonalnej — będącej odwrotnością obiektu G_ob‘(s) uzupełnionej czynnikam® 1/(1 +sT_i}) w celu osiągnięcia realizowalności regulatora. Stałe T_;J powinny być współ* mierne ze stałymi czasowymi obiektu. Elementy części diagonalnej regulatora projektuje się standardowo dla kolejnych obwodów regulacji, traktując je jako samodzielne obwodv [8.16],

W przypadku obiektu nieminimalnofazowego regulator odprzęgający projektuje się zakładając niezerowe transmitancje na przekątnej transmitancji macierzowej układu zamkniętego. Pozostałe elementy tej macierzy przyrównuje się do zera. Rozwiązania otrzymanego układu równań z q~ niewiadomymi są elementami transmitancji macierzowej regulatora odprzęgającego. W przypadku trudności z ich realizowalnością należy zmodyfikować transmitancję układu zamkniętego i ponownie wyznaczyć transmitancje regulatora wielowymiarowego.

8.6.2. Regulatory optymalne

Regulatorem optymalnym jest nazywany regulator minimalizujący — w przestrzeni sterowań dopuszczalnych 9l_u. ueS, — wybrany wskaźnik jakości regulacji, np. czas regulacji, całkę z kwadratu uchybu, całkę z modułu uchybu, całkę z kwadratu zmiennych stanu i sterowania itp. Ogólnie, wskaźnik jakości składa się z dwu części: części określającej koszt działań dynamicznych (reprezentuje ją całka) i części określającej koszt działań statycznych,

(8.30)

J(u,x,t) = jF(x,u,t)dt+G(x,u,t)lo

gdzie: t — czas; 0 i i_k — chwila początkowi i końcowa; u ix — zmienne sterowania i stanu. Część statyczna jest istotna, np. przy optymalizacji napędu synchronicznego, gdzie chodzi nic tylko o odpowiednią dynamikę, ale i o optymalną statykę (minimum mocy).

Funkcjonał jakości J i równania stanu procesu sterowanego określają zadanie optymalizacji regulatora. Zadania takie można rozwiązać metodami: rachunku wariacyjnego, programowania dynamicznego Bcllmana (zasada optymalności) lub za pomocą zasady maksimum Pontriagina [8.3; 8.6; 8.12]. W projektowaniu regulatorów optymalnych najczęściej wykorzystuje się zasadę maksimum Pontriagina lub zasadę optymalności.

Według zasady optymalności, jeżeli trajektoria układu sterowania jest optymalna w przedziale czasu [0, t_t], to każda jej część końcowa odpowiadająca przedziałowi czasu [t i, f_t] jest optymalna. Jeżeli w chwili tj > 0 układ znalazł się z jakichkolwiek przyczyn w' punkcie P, na trajektorii optymalnej i jeśli od chwili t, (aż do osiągnięcia PJ ma działać optymalnie, to jego trajektorią musi być prawy odcinek linii ciągłej (rys. 8.2oaj-W metodzie projektowania dynamicznego Bellmana wykorzystuje się zasadę optymalności w taki sposób, że obliczenia optymalizacyjne prowadzi się wstecz, zaczynając poszukiwania punktu leżącego na końcowym odcinku trajektorii optymalnej [o-¹J (punkt a na rys. 8.26b). Programowanie dynamiczne jest szczególnie efektywne w układa dyskretnych lub zdyskretyzowanych. Pomiędzy kolejnymi punktami decyzyjnym¹ l^ry 8.26b) sterowanie jest stałe. Poszukiwanie optymalnego sterowania od P„ do .* rozpoczyna się od znalezienia punktu a, a następnie b, c itd. aż do P„. Jest to szczegom efektywna metoda w zadaniach optymalizacji z ograniczeniami.    j_a:

Zasada maksimum Pontriagina podaje warunek konieczny optymalności sterów* sterowanie tf e układu opisanego równaniem stanu i - f(x, u) jest optymalne w sc

wskaźnikajakości J = J/₀(x,«)dt, jeżeli hamiltonian H = — f₀+f_l\p_i + ... +/„'/'n

funkcją sterowania H(u) osiąga maksimum przy u = u° [8.4; 8.6; 8.12], przy czym ⁱ

0)

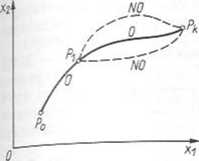
Rys 8.26- Ilustracja metody programowania dynamicznego; a) zasada optymalności; b) wyznaczanie sterowania optymalnego

0 tfO _ trajektoria optymalna i nieoptymalna; P₀, P_k - punkt początkowy i końcowy (docelowy); .t,, x₂ - zmienne stanu

a—zmienne stanu sterowania; H(«“) = 0;/ =    >•••></'„ — sprzężone zmienne

stanu; t — chwila końcowa; T — znak transpozycji.

Zasadę tę wykorzystuje się do projektowania regulatora LQR (ang. Linear Quadratic

00

Regulator) minimalizującego kwadratowy wskaźnik jakości J = j (x^TQx + u^l Ru)dt, jeśli

o

prawo sterowania u = — Kx, przy czym: Q, R — macierze symetryczne dodatnio określone; K—macierz wzmocnień regulatora. Jeżeli obiekt sterowania opisuje równanie x = Ax + Bu, to wzmocnienia regulatora minimalizujące J określa macierz K = R~ ¹B^TP, przy czym P—macierz symetryczna, dodatnio określona, jest rozwiązaniem macierzowego równania Riccatiego [8.6]

A^TP+PA + Q-PBR-'B’ P = 0    (8.31)

Zastosowanie regulatora LQR jest możliwe w przypadku mierzalności wszystkich zmiennych stanu. Jeżeli zmienne stanu x nie są dostępne, to należy zastosować obserwator stanu, który na podstawie sygnału >’(r) odtworzyje (jeśli obiekt jest obscrwowalny). Zwykle wyniki pomiarów sygnałów y(t) są obarczone szumami i do odtwarzania stanu stosuje się optymalne filtry Kalmana-Bucy (KBF) [8.6], minimalizujące błąd średniokwadratowy między estymatą x(t) i wartością estymowaną jc(f). Równania obserwatora KBF są następujące: x = Ax + Bu + P(y—y), y = Cx, przy czym P = SC⁷W¹, macierz S spełzając warunek SS^T > 0 jest rozwiązaniem równania Riccatiego AS+SA^T+8— ~SC A' 'CA = 0, gdzie 1\i 6 — macierze kowariancji zakłóceń pomiarowych działających na obiekt [8.6]. Regulator zawierający KBF i LQR jest nazywany regulatorem LQG (ang. Linear Quadratic Gaussian). Procedury komputerowego projektowania filtrów KBF oraz regulatorów LQR i LQG są dostępne np. w programach PC-Matlab i CC [8.23; 8.32]. ■ . Instalacje technologiczne jako obiekty typu MIMO zazwyczaj mają charakterystyki [.^(wydajność, zysk, sprawność) typu ekstremalnego. Położenie ekstremum zależy od _sv!^c *°ści regulowanych i od zakłóceń działających na proces. Optymalizacja takiego akt i^U P°*^e§^{a na} bieżącym wyznaczaniu zespołu sygnałów zadanych odpowiadających ualnemu położeniu ekstremum wskaźnika jakości instalacji i zadawaniu ich powolnym regulatorom [8.12; 8.31],

^•3. Regulatory adaptacyjne

^lrach ^at°^ry ^adaPtacyjne stosuje się do sterowania obiektów o zmieniających się parame-z^i .ⁿP- do sterowania robotów, do sterowania reaktorów, które na skutek starzenia *£>»« parametry itp. W układzie sterowania adaptacyjnego (rys. 8.27a) na bieżąco 5 pokonywać identyfikacji parametrów a obiektu i na podstawie ich estymat obi_ei_cl^eDlad nastawy regulatora. Regulatorami adaptacyjnymi są więc: identyfikator ^tu> przelicznik nastaw regulatora i regulator o nastawialnych parametrach.