4497

?o

Siukany zbirfr skład* się ■ punktów /. kldrych odbgłoM od pukla «| ■ —J jest nic msltjin mii odległość od J

Liczby

punktu ma

= 2i Jest lo latem pdłpłasi-

csjsaa agrtiKioia lymctralną odcialta o końcach i). i». ba punktu <| • 2«. Sjadraha la aalesy do Mukaargo | zbioru (asbsci rysunek).

#) Po»z u kiwany ibtdr jol wspólną Cię. toą skśorów okfrńJoayrk przez «i-ranki:

Jte(i+ 1) <0. li- sl ś 3.

Pirrwmy mnack określa lewą pól-płaasciyinę otwartą ogranicioną pro-slą » -f I « 0. Dragi warunek okraja koło domknięte o środku w punk-oe a ^s i i promieniu r = 3 Wspólną część tych i Worów pncdilawiono na rysunku.

Im ■

f) Mamy

|<* + 2.)(a-2.)|<|z-2.| |a + 2.|-|*-2i|<|»-2.|

|r - 2i| — O albo |i — 2ij > 0 oraz |< + 2i| < 1.

• Im a j

R« .

Waraack

|r-2lj = 0

wynaacza ibiór (2i), a warunki

|r + 2i| < 1 oraz |r — 2i| > 0

określają kolo domknięte o środku w punkcie an a —2i i promieniu r = 1.1 Sumę tych zbiorów przedstawiono na rysunku.

Przykład 2.3

Znaleźć najmniejszą i największą wartość modułu liczby zespolonej J^r/r 1

\t - A + 3t| <

O rugi tydzień - przyktndy

21

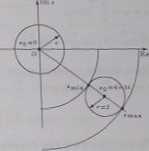
Rozwiązanie

Zbiór liczb zespolonych z spełniających nierówność |z — t t- 3i| ^ 2 jest kołem domkniętym o środku w punkcie xo = 4 — 3i i promieniu r m 2. Zbiór liczb zespolonych spełniających równanie |z| = e, gdzie o > 0, jest okręgiem o środku w początku układu współrzędnych i promieniu c. Promień e będzie najmniejszy, największy, gdy okrąg |*f = e będzie styczny odpowiednio zewnętrznie, wewnętrznie z okręgiem |z — ■! + 3i| a 2. Zatem najmniejsza, największa wartość |z| jest równa

|*min| — |*01 — i' - |4 — 3i| — 2 = 3,

|z«>«| = |«o| + r = |4 - 3t| + 2 = 7.

• Przykład 2.4

Podane liczby zespolone zapisać w postaci trygonometrycznej:

fi) -$Ę>    b) -6 + 6i;    c) —2t;    d) >/3 + i;

c) sina — i cos a; f*) 1 + cos a + i sin a; g) 1 — ictga.

Uwaga, W ćwiczeniach e), f*), g) kąt a spełnia nierówności 0 < o < ~. Rozwiązanie

Każdą liczbę zespoloną z można zapisać w postaci trygonometrycznej:

z = r (cos + i sio <p),

gdzie r jest modułem, a <p argumentem liczby z.

a)    Dla z = —y/b mamy r = \/5 oraz V = «• Zatem

—y/Ś k \/s (cos ir + i sin x) .

b)    Dla z ■= —.(i + Ci mamy r = 6\/2 oraz ip a Zatem

-6+6i a S\/2 ^cos ^ + i sin    -

c)    Dla z *= — 2i mamy r = 2 oraz

3zr „

¥>= -y. óatem

-²ⁱ - * («• y+ ■'*£)•