70(1) 2

7. PLANIMETRIA

Obliczamy sumę miar kątów.    a + fi = 20‘ + 40* = 60*

Obliczamy różnicę miar kątów.    fi - a = 40* - 20* = 20*

Odpowiedź: D.

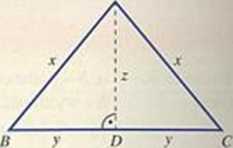
Trójkąt ABC jest równoramienny, AD jest jego wysokością i | AB \ = |/\C'| Obwód trójkąta \f)ę) 30. a obwód trójkąta ABC jest równy 36. Długość odcinka AD jest równa:

A. 10    B. 6    C. 12    D. 13

Rozwiązanie:

Wykonujemy rysunek pomocniczy.

Korzystając /. oznaczeń na rysunku, zapisujemy odpowiednie równości.

Z drugiej równości wyznaczamy .v + >•.

z + y + x - 30 x + y + y + .v = 36

Do pierwszej równości wstawiamy 18 w miejsce ,v + >■ i obliczamy z. czyli wysokość trójkąta.

x + y + y + .v = 36 2* + 2y = 36    |: 2

x + .y = 18

z + >• + .v = 30 z + 18 = 30 Z =30- 18 z = 12

Odpowiedź: C.

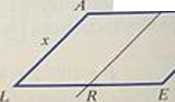
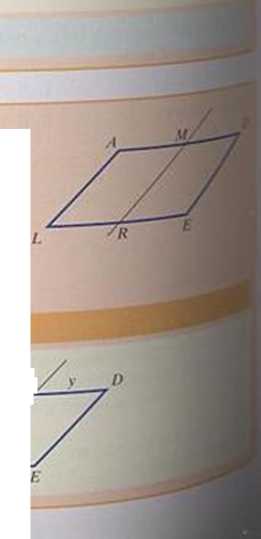
Równolcglobok ADEL przecięto na pól prostą MR, otrzymując dwa rów* nolcgloboki podobne do równolcgloboku ADEL Stosunek długości krótszego boku do długości dłuższego boku równolcgloboku AMRL jest równy:

A./2

¹Ą

d.4

Rozwiązanie:

Oznaczmy boki równolcgloboku: .v. 2y.

Równolcglobok ADEL jest podobny do równolcgloboku AMRL

y M.

Mv

■BSwicdnich

BF*^w..głołHikó'v JCM

rJużs^ni b<’^kic,n nł^^j^obokii '^K,,<!

_ £

.v^:= 2y^:

.v = Ą y

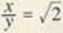
_fottoaal_Camy«pi^K"’^;!

Rytytf dodatnia, więc

-.rany niania.

Odpowiedź: A.

Punkt i? jest środkiem kota. Obwód zacienionej figury jest równy: JL« + Ip5    C. 1271 + 3/3

Ł43t6,5    D.43 + 3,/3

Rozwiązanie:    _t

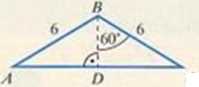
OłmtnJ figury jest sumą odcinka,' będącego bokiem trójkąUi i luku okręgu.

Obliczamy najpierw długość ^N,ku DC trójkąta ABC. Bg/^Cjest równor.unMim. y*~**^BDlcż> na dwusiee/nej

^{2 f}.^UnkcJi Mnu.s. aby ^fftogOŚĆ odcinka DC.

bierze |2o*    ,

^wyznae/a luk stanowiący 4£jyr = \ długości okręgu.

Odcinek Ar ■

SS^ld"^;i raz, odcinka /,

\DC\

sii i60* =

/3 | DC\

2 ~ 6 21 /JC| = 6_%/3 \DC\ = 3,/3

| AC| = 2 • 3/3 = 6^3