Capture123

Rozważmy następny przykład. Tabela 13.6 przedstawia dane zebrane Woo (1928) na temat związku między „ocznością" i „ręcznością" w próbie 413 osób badanych. Każdą osobę badano pod względem „oczności" i ..ręcznoścf. po | czym przydzielano ją do jednej z trzech kategorii w zakresie obu zmiennych Da każdej osoby otrzymano zbiór par pomiarów Tabela 13.6 jest tabelą wielod/n dla 413 par pomiarów. Liczebności oczekiwane w poszczególnych kutk.wh obtoczono. mnożąc przez siebie sumy / odpow iednich wierszy i kolumn i dzieląc

r«M> 13.7. OWowii Z^: dli danych z ubcli |J*

O-F.	(O - ty	(O-O* £
-L4	1.96	0.055
3.5	12.25	0209
-2.0	4.(¥)	0.133
5.6	3136	1.465
-7.4	54.76	I.M7
1.8	3.24	0.178
-4.1	16.81	0.275
4.0	16,00	0.158
(U	004	0.001
		y; * 4.021

WamM V wynosi iu 12.70 lk stopni swobody je%t /ui.t/.imdi / _x^: ' W ka/dci tabeli 2x2. przy ograniczeniach wyrokujących / sum h,_/c t\lko jedno pole może się swobodnie zmieniać W powyższej pr^> kł.ij,,_Wc,,

: x 2 zaobserwowana liczebność kratki \,/ł_: wynosi 50. Jeżeli znani> i_c i_;,_/( a sumy brzegowe są ustalone, to wszystkie pozostałe liczę hno-U., ^ „_w ^ Liczebności A\B_:. A?B\ i A_:B_: otrzymujemy przez proste odejmowanie jedna kratka może się swobodnie zmieniać. Wartość X’ wymagana dla    I

poziomie 0.05 przy Jf= I wynosi 3.84. a dla Istotności na poziomie 0.01 uvrv,_M Otrzymana wartość x^:= 1-70 przekracza wartość wymagana dla    _r,₁₍

ziemie 0.01. Oczywiście A nie jest niezależne od B Można twierdzi, ,_c A i B istnieje związek.

Dla każdej tabeli 2x2. przy danych sumach brzegowych, liczba M,.p_n. body związana z wartością y; równa jest I. Ogólnie rzecz biorąc, dla dow«.inq_t o R wierszach i C kolumnach liczba stopni swobody związana z wartością danych sumach brzegowych, równa jest (R - 1)(C - I). Zatem dla tabeli v,i| liczba stopni swobody wynosi (3 - 1)<2 - l)= 2 Czytelnik z łatwością mmi że w przypadku każdej tabeli 3x2. przy danych sumach brzegowych jczcl> liczebności są znane, to pozostałe cztery są ustalone i nie mają żadnej nJ zmieniania się.

Tabela 13.6. Tabela wiclodzKlCza ukazująca związek między latcraliza cją ocni i rąk w próbie 413 o*6b badanych oraz obliczenia wartości oczekiwanych

	Leworęczni	Oburęczni	Praworęczni	Razem
Leworęczni	34	62	28	124
	(35.4)	(58.5)	(30.0)
Oburęczn,	27	28	20	75
	(21.4)	(35.41	08,2)
Praworęczni	57	105	52	214
	(61.1)	(101.0)	(51.8)
Razem	118	195	100	413
Obliczenie wartość, oczekiwanych
I24x 118	, 124x 195		124 x 1(X)	= 30.0
413	35.4 —= 58.5		413
75x 118 75 x 195 413 413 '			75 x 100 413	= 18.2
214 x IIH	214 x 195		214 x100 413	« 51.8
“41“ ^=	61.1 —J\3~~ ^= lt>1.0

iW»yn p>«* «"hę pomlunkw Lic/eim,*, , . pduw w nMi w nawias,u. I,    , p.«,_c«.^_nv .

¹ _leKli lalerali/acja ik/.u , r;,k    w«_Km„_lc , ,

„ , pterw.«r* wim« r.„l„„ _{uc w} ^    '«»* ""/ale**.    ,,,

kolumn W«!Bfc_iocMllwjn<;    ->n,    *

^,r'^cch » tej kolumnie . JT’¹'' * ' <***£ Wmtofc octekiwanc 15.4. 21 4 , _M    f*"potej..rm_r,. .<.

, .*«> U*. » • ²¹⁴ PWlohnc ulernow, _pr„ ’    *    ' ' " ■    J.,

owkiwme tetaoic, w krad^j, pm/c,^'* '* *>^^1 *

uMi .Kk»l«te/rj .4 proporcjonalne do _lum    , k,,|_um„

nbełl 13 7 przedstawia obliczem., /• jj. _llłn ‘ . ^>th

I    * ^U,J «**>«»» ' tabel, 1 j f,

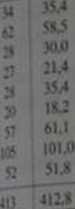
Otrzymana wartość r wynos. 4.021. Liczba siopn. swobody związana , _u ul«4 równa    IMC - l) = (3 - 1M3 - 1)^4. Wanośc    ^

wottoŃi na poziomic 5 procom wynos, 9.488. Nic mam; ratem pod,u* do od-mama hipotezy o wzajemnej niezależności latcralizacj, oczu i _r* Najwyrażn*, łnk jot związku między tymi dwiema zmiennymi.

13.6. Obliczanie dla tabeli 2x2

Często spotykaną postacią tabeli wieiodzielczej jest czteropolowa tabela 2x2 Test niezależności z użyciem x^: można łatwo przeprowadzić bez obliczania wartości auAiwanych. Przedstawmy liczebności w polach oraz liczebności brzegowe w ustępującej postaci:

243

242