CCF20090120057

baty. Teraz mamy dwie informacje dotyczące cen ciastek i bułek:

b + 2c = 5 26 + 5c = 12

Jeśli 1 bułka i 2 ciastka kosztują 5 zł, to dwa razy więcej — 2 bułki i 4 ciastka — musi kosztować 2 razy tyle, a więc 10 zł. Ale napisaliśmy przed chwilą, że 2b + 5c = 12, wobec tego z porównania obu równań wynika, że c = 2. W takim razie b = 1. Wracając do informacji o pierwszym posiłku, dowiemy się, że h — 3.

Taką stenografią można się również posługiwać przy opisie faktów. Od dawina znana jest następująca zabawa: „Pomyśl sobie jakąś liczbę. Dodaj do niej 6. Pomnóż wynik przez 2. Odejmij 8. Podziel przez 2. Odejmij licżbę, którą pomyślałeś na początku”. Jakakolwiek by to była liczba, odpowiedź zawsze będzie brzmiała: zostało 2. Dlaczego?

Można rozpatrzyć to zagadnienie myśląc konkretnymi obrazkami. Pomyśleliśmy jakąś dowolną liczbę. Możemy ją sobie wyobrazić jako kulki umieszczone w woreczku. „Dodaj do niej 6”. Mamy teraz jeden woreczek i sześć-kulek luzem. „Pomnóż przez 2” — dwa woreczki i dwanaście kulek. „Odejmij 8” —- dwa woreczki i cztery kuliki. „Podziel przez 2” — jeden woreczek i dwie kulki. „Odejmij liczbę, którą sobie pomyślałeś na początku” — a więc zabierz woreczek. Pozostają dwie kulki — bez względu na to, ile kul Ok znajdowało się w woreczku.

W algebrze nie mówimy o woreczkach i kulkach. Mówimy: niech n oznacza dowolną liczbę, jaką zechcesz pomyśleć. „Dodaj 6” — mamy n-\~6. „Pomnóż przez 2” — 2n+12. „Odejmij 8” — 2n + 4. „Podziel przez 2” — n+2- „Odejmij n” — pozostaje 2.

Wszystkie te czynności wraz z faktem, że od-

ZAPIS SŁOWA OBRAZKI ALGEBRAICZNY
I. II. III.	Pomyśl sobie pewną liczbę	0	ń
	Dodaj do niej 6	V J o 0 o o o o	71 +6
	Pomnóż wynik przez 2	n- O O O o o o 0 \—J o o o o o o	2(n+6)> czyli 2n-M2
IV. V.	Odejmij 3	aa o o o o 1	2(n+6)—8, czyli 2n+4
	Podziel przez 2	o o D	2(n+6)-8 2 ra+2
VI.	Odejmij od tego liczbę, którą pomyślałeś na początku	O O	2(n+6) —8 -'--n 2 czyli 2 \
VII.	Otrzymałeś 2	o o	2(n+6) —8 „ 2 ^71 2*

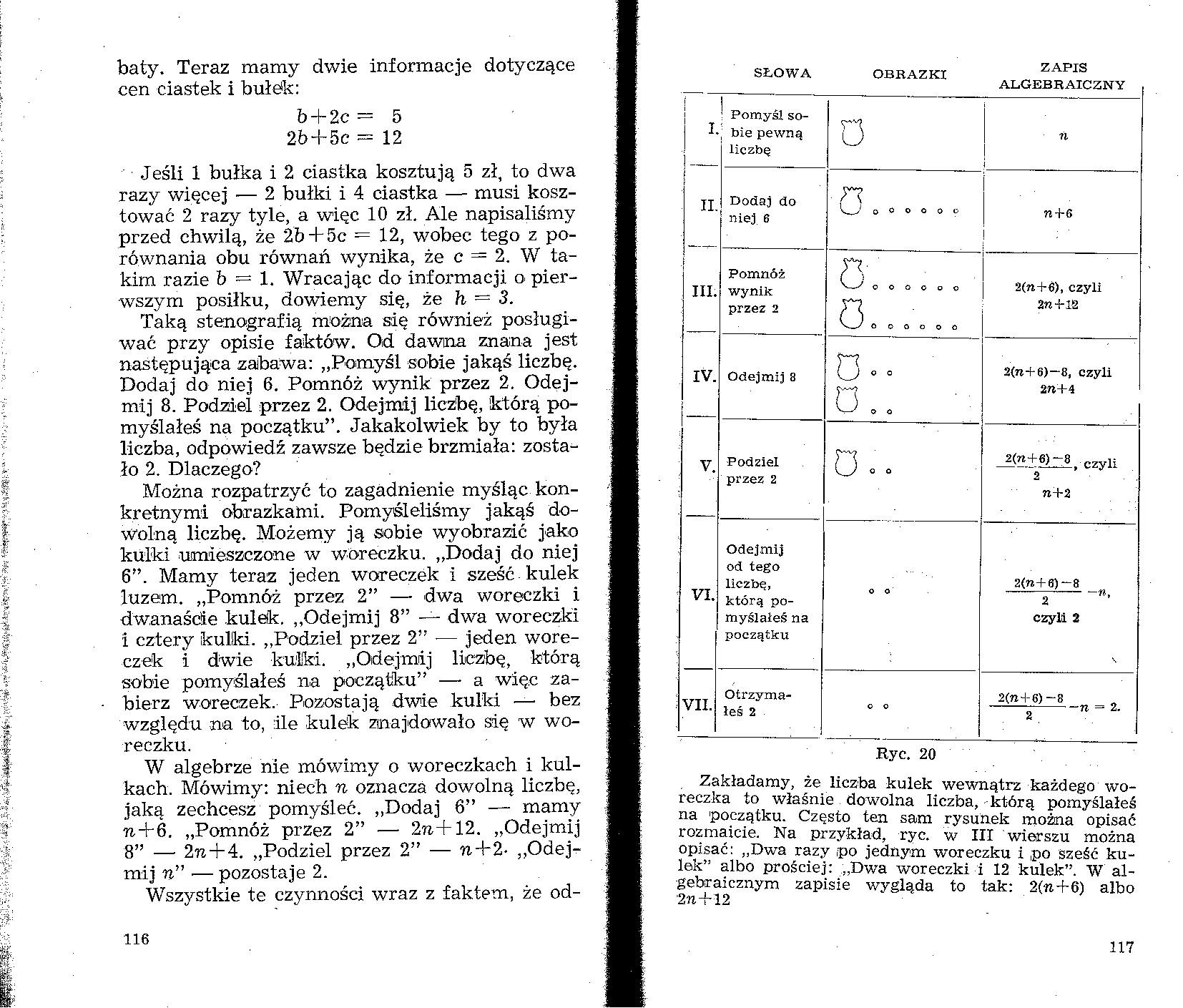
Ryc. 20

Zakładamy, że liczba kulek wewnątrz każdego woreczka to właśnie dowolna liczba, którą pomyślałeś na początku. Często ten sam rysunek można opisać rozmaicie. Na przykład, ryc. w III wierszu można opisać: „Dwa razy ,po jednym woreczku i ,po sześć kulek” albo prościej: „Dwa woreczki i 12 kulek”. W algebraicznym zapisie wygląda to tak: 2(n+6) albo •2n-M2

117