CCF20090120117

TRYGONOMETRIA, CZYLI JAK PRZEBIJAĆ TUNELE I SPORZĄDZAĆ MAPY

„Trzeba dokładać największych starań, aby uniknąć błędów; dowodem, że starań tych dołożono, jest cudowna zgodność, z jaką zazwyczaj schodzą się drążone z przeciwnych końców tunele... Tunel Musconetcony ma około 5000 stóp długości. Gdy .drążone z przeciwnych końców jego części zeszły się, stwierdzono, że błąd w kierunku tuneli wyniósł pół cala, a błąd w poziomie — zaledwie jedną szóstą cala. Przy budowie tunelu Hoosac, o długości 25 000 stóp, błędy te były jeszcze mniejsze”.

A. Wiliams Victories of the Engineer

W książce tej starałem się udowodnić, że: 1) problemy matematyczne można sformułować w języku potocznym; 2) każdy człowiek może próbować rozwiązywać te problemy posługując się zdrowym rozsądkiem; 3) metody podawane w podręcznikach są po prostu ulepszeniem początkowego podejścia opartego na zdrowym rozsądku; ulepszenie to osiągano stopniowo, dzięki pracy całych pokoleń matematyków.

W żadnym dziale matematyki nie można pokazać tego prościej niż w trygonometrii. Trygonometria wyrasta z bardzo prostych zagadnień praktycznych, takich np. jak budowa tunelu-kolejowego. Może zajść potrzeba przebicia tunelu, którego drugi wylot ma znajdować się wiele km od danego pudktu, po przeciwnej stronie pasma gór, w miejscu, którego nawet nie widać z tej strony gór. Może zajść potrzeba drąże-na tunelu z obu jego końców jednocześnie, tak aby przekopy spotkały się gdzieś pod górą. Jak wyznaczyć właściwy kierunek drążenia?

Jedną metodę podaje E. B. Schieldrop w rozdziale 4 swojej książki The Railway. Metodę tę ilustruje ryc. 42. Część zakreskowana przedstawia obszar górzysty. Punkty A i D należy połączyć tunelem. Możemy znaleźć 'takie obiekty B i C, aby obiekt B był widoczny z punktu A, obiekt C był widoczny z obiektu B, a punkt D z obiektu C. Mierzymy starannie długości i kierunki odcinków AB, BC i CD.

B

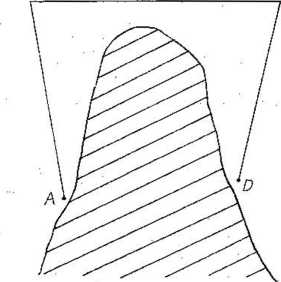
Ryc. 42

C

To wystarczy do ustalenia położenia punktu D. Możemy sporządzić mapę okolicy, w skali, powiedzmy, 1 cm do 1 km. Na mapie tej możemy zaznaczyć punkty A, B, C i D. Zaczynamy od punktu A i rysujemy kolejno odcinki od A do B, od B do C, od C do D we właściwych kierunkach i w obranej skali. W ten sposób ustalamy położenie punktu D. Na mapie możemy narysować odcinek AD i zmierzyć kąty, jakie tworzy on z odcinkami AB i CD. Wiemy więc już,

237