CCF20090120124

na morzu przez ustalanie jego położenia względem dwu latarni morskich, przy lokalizowaniu łodzi podwodnych itd.

Mierniczowie i żeglarze są w tym szczęśliwym położeniu, że mogą kupić sobie drukowane tablice zawierające wartości sinusa i cosdnusa oraz inne informacje. Ale ktoś przedtem musiał te tablice sporządzić — i sprawa sporządzenia tablic jest naszym drugim zagadnieniem; właśnie w związku ze sporządzaniem tablic odkryto pewne własności sinusa i cosinusa. Zainteresowanie matematyków XVI w. algebrą częściowo spowodowane było faktem, że równania trzeba było rozwiązywać, zanim można było sporządzić tablice trygonometryczne.

Po trzecie wreszcie, pożądana jest znajomość własności sinusa ^!i cosinusa z powodów zupełnie ogólnych. W wielu zagadnieniach występuje sinus i cosinus i często pracę można sobie znacznie uprościć i skrócić, jeżeli zna się odpowiednie wzory. Przykład takiego uproszczenia podamy później.

TWIERDZENIE PITAGORASA

Na ryc. 44 boki OQ i QP mają długości cos t i sin t, gdzie t jest wielkością kąta QOP. Uczniowie zazwyczaj z dużą łatwością przyswajają sobie tę zależność, ale nie zawsze rozpoznają ją, gdy pojawi się ona w innym położeniu albo w innej skali. Na przykład, na ryc. 46 bok DF tworzy kąt t z bokiem DE, a bok DF ma długość 1. Odcinek EG poprowadzono pod kątem prostym do boku DF. Łatwo spostrzec, że trójkąt DEF ma ten sam kształt, co trójkąt OQP, ale może już nie być tak oczywiste, że na tym rysunku występują jeszcze dwa trójkąty o tym samym kształcie. A tak właśnie jest. Jeżeli wytniemy

z papieru trójkąty przystające dokładnie do trójkątów DEG i FEG, to zauważymy, że trójkąty te można" (po odwróceniu ich) umieścić odpowiednio w położeniu LVW i LTU. Trójkąt LMN ma dokładnie tę samą wielkość i kształt co trójkąt DEF. Obecnie jest oczywiste, że wszystkie trzy trójkąty mają ten sam kształt, a różnią się tylko wielkością.

c    N

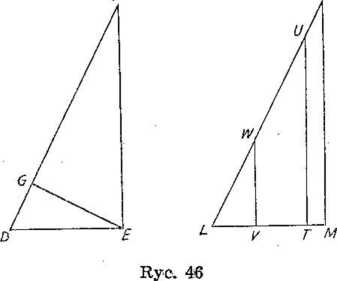
Jaka jest długość odcinków DG i GF? Odcinek DG można umieścić w pozycji LV, a więc długość jego wynosi cos t razy LW. Ale odcinek LW ma tę saimą długość oo odcinek DE, który jest równy cos t. Zgodnie z tym odcinek DG musi być równy cos t razy cos t, czyli (cos t)². Dokładnie w ten sam sposób można wykazać, że odcinek GF ma długość (sin t)³. Ale odcinki DG i GF tworzą w sumie odcinek DF, który narysowaliśmy na samym początku jako odcinek o długości 1. Wynika stąd, że

(cos t)²+(sin t)² = 1.

W rozdz. 2 spotkaliśmy się z trójkątem o bokach 3, 4 i 5 i o kącie prostym pomiędzy bokami 3 i 4. Jeżeli narysujemy ten trójkąt w skali

251