DOBRZANSKI 027

Tabl. 3.1 Icd.)

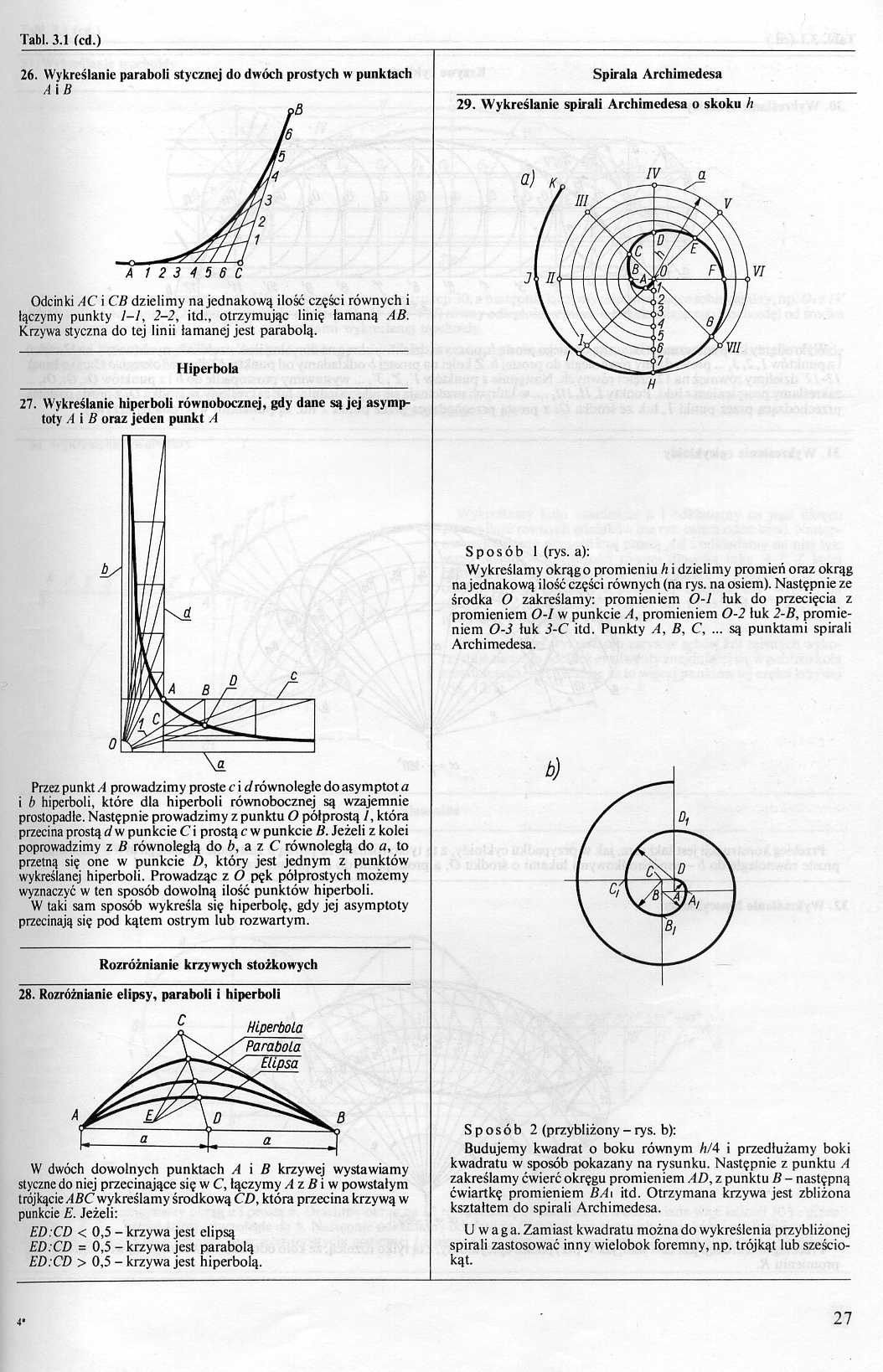
26. Wykreślanie paraboli stycznej do dwóch prostych w punktach

Spirala Archimedesa

A i B

27. Wykreślanie hiperboli równobocznej, gdy dane są jej asymp-toty A i B oraz jeden punkt A

Sposób I (rys. a):

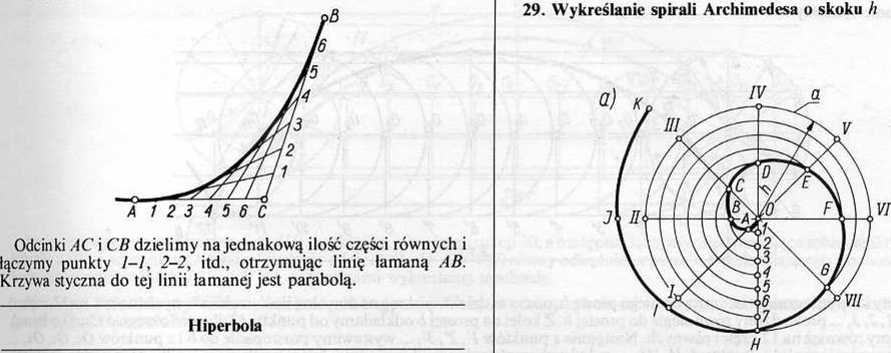
Wykreślamy okrągo promieniu h i dzielimy promień oraz okrąg na jednakową ilość części równych (na rys. na osiem). Następnie ze środka O zakreślamy: promieniem 0-1 luk do przecięcia z promieniem 0-1 w punkcie A, promieniem 0-2 luk 2-B, promieniem 0-3 tuk 3-C itd. Punkty A, B, C, ... są punktami spirali Archimedesa.

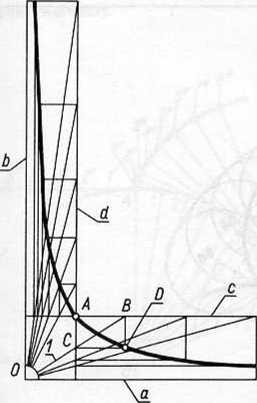
Przez punkt A prowadzimy proste c i drównoległe do asymptot a i b hiperboli, które dla hiperboli równobocznej są wzajemnie prostopadle. Następnie prowadzimy z punktu O pólprostą /, która przecina prostą d w punkcie Ci prostą c w punkcie B. Jeżeli z kolei poprowadzimy z B równolegtą do b, a z C równoległą do a, to przetną się one w punkcie D, który jest jednym z punktów wykreślanej hiperboli. Prowadząc z O pęk pólprostych możemy wyznaczyć w ten sposób dowolną ilość punktów hiperboli.

W taki sam sposób wykreśla się hiperbolę, gdy jej asymptoty przecinają się pod kątem ostrym lub rozwartym.

Rozróżnianie krzywych stożkowych

28. Rozróżnianie elipsy, paraboli i hiperboli

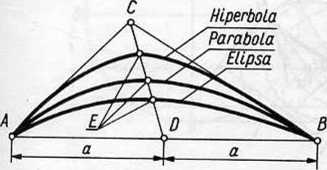
W dwóch dowolnych punktach A i B krzywej wystawiamy styczne do niej przecinające się w C, łączymy A z B i w powstałym trójkącie ABC wykreślamy środkową CD, która przecina krzywą w punkcie E. Jeżeli:

ED.CD < 0,5 - krzywa jest elipsą ED.CD = 0,5 - krzywa jest parabolą ED.CD > 0,5 - krzywa jest hiperbolą.

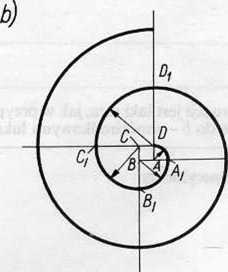
Sposób 2 (przybliżony - rys. b):

Budujemy kwadrat o boku równym h/4 i przedtużamy boki kwadratu w sposób pokazany na rysunku. Następnie z punktu A zakreślamy ćwierć okręgu promieniem AD, z punktu B - następną ćwiartkę promieniem BAi itd. Otrzymana krzywa jest zbliżona ksztattem do spirali Archimedesa.

U waga.Zamiast kwadratu można do wykreślenia przybliżonej spirali zastosować inny wielobok foremny, np. trójkąt lub sześcio-kąt.

4*

27