DOBRZANSKI 029

Tabl. 3.1 (cd.)

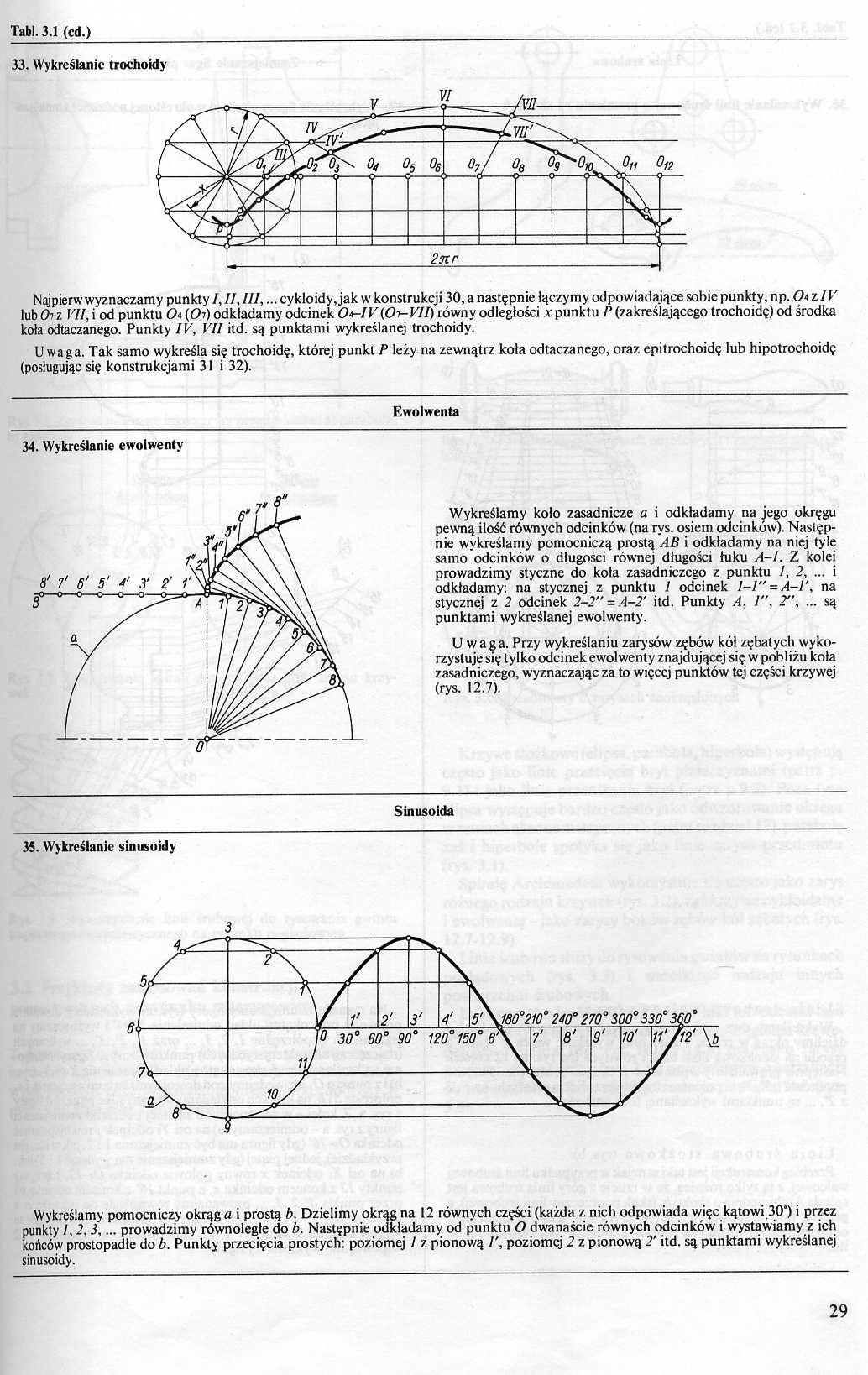
33. Wykreślanie trochoidy

Tabl. 3.1 (cd.)

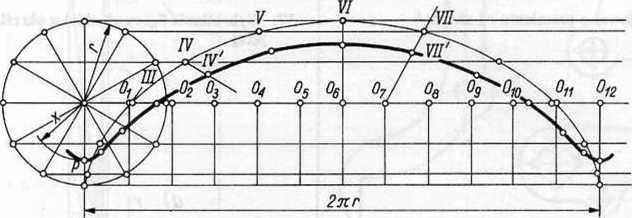
Najpierw wyznaczamy punkty /, //, III,... cykloidy Jak w konstrukcji 30, a następnie łączymy odpowiadające sobie punkty, np. O* z IV lub Oi z VII, i od punktu Oi (Ch) odkładamy odcinek O*-I V(Ch- VII) równy odległości x punktu P (zakreślającego trochoidę) od środka koła odtaczanego. Punkty IV, VII itd. są punktami wykreślanej trochoidy.

U waga. Tak samo wykreśla się trochoidę, której punkt P leży na zewnątrz kota odtaczanego, oraz epitrochoidę lub hipotrochoidę (posługując się konstrukcjami 31 i 32).

Ewolwenta

34. Wykreślanie ewolwenty

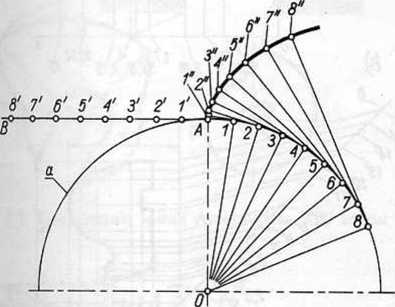
Wykreślamy koło zasadnicze a i odkładamy na jego okręgu pewną ilość równych odcinków (na rys. osiem odcinków). Następnie wykreślamy pomocniczą prostą AB i odkładamy na niej tyle samo odcinków o długości równej długości łuku A-I. Z kolei prowadzimy styczne do koła zasadniczego z punktu I, 2, ... i odkładamy: na stycznej z punktu I odcinek I-I" = A-l', na stycznej z 2 odcinek 2-2" = A-2' itd. Punkty A, I", 2", ... są punktami wykreślanej ewolwenty.

Uwaga. Przy wykreślaniu zarysów zębów kół zębatych wykorzystuje się tylko odcinek ewolwenty znajdującej się wpobliżu kola zasadniczego, wyznaczając za to więcej punktów tej części krzywej (rys. 12.7).

Sinusoida

35. Wykreślanie sinusoidy

3

Wykreślamy pomocniczy okrąg a i prostą b. Dzielimy okrąg na 12 równych części (każda z nich odpowiada więc kątowi 30') i przez punkty 1,2,3,... prowadzimy równoległe do b. Następnie odkładamy od punktu O dwanaście równych odcinków i wystawiamy z ich końców prostopadłe do b. Punkty przecięcia prostych: poziomej l z pionową /', poziomej 2 z pionową 2' itd. są punktami wykreślanej sinusoidy.

29