DSC00091 3

adanie I

Zadania domowe seria 1

B

l.ing* AB (nieskończenie cienki pręt)poddano deformacji opisanej polem pr/ernies/c/en u . v :

u(x) = (5+    [mm];

v(x) = (2 +    |mmj;

gd/ie 1= (100+ 3D) |cm|;

1.    Narysować pręt AB po deformacji.

2.    Określić pola odkształceń, tzn. wyliczyć funkcje określające składowe tensora Cauchy’ego G_x(x), C_y(x), Yxy (x) (tylko człony liniowe pochodnych przemieszczenia).

3.    Wykreślić odkształcenia z powyższego punktu.

4.    Wykreślić odkształcenie £_x(x) obliczone jako składowe tensorów Cauchy’ego i Greena.

Zadanie 2

c

Prostokątną tarczę ABCD poddano deformacji opisanej polem przemieszczeń u , v :

A

h

« V x_>

u(x,y) = (5 + A)*(j) (mm);

v(x, y) =(2 + B)*( j) [mml; gdzie ł= (100 + 3D) JcmJ;

1.    Narysować tarczę ABCD po deformacji.

2.    Określić pola odkształceń, tzn. wyliczyć funkcje określające składowe tensora Cauchy’ego £_x(x,y), £y(x,y), y_xy (x,y) (tylko człony liniowe pochodnych przemieszczenia).

3.    Wykreślić odkształcenia z powyższego punktu wzdłuż boków AB i CD.

Zadanie 3

B

Linę AB (nieskończenie cienki pręt) poddano

deformacji opisanej polem przemieszczeń u , v u(x)= ? ;

n%

v(x) = (10 + D)(-l)^fcsin — [mm];

gdzie 1= (100+ 3B) (cmj;

Wiadomo, iż pręt tak zdeformowano, że ostatecznie dla całego przedziału x e <0, I) odkształcenie ₂C_x(x)=0. Korzystając z uproszczonej postaci składowej £_x(x) tensora Greena

Wskazówka.

wyznaczyć przemieszczenie u(x).

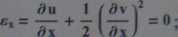
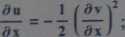
oraz u(x) =

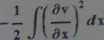
1. Narysuj pręt po deformacji.