DSCI8748

Zestaw I

WAMI*    AiyjM

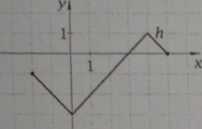
1. Poniżą) podano trzy funkcje. Dla każdą) z nich ustal:

a)    Jaka Jest dziedzina funkcji?

b)    Jaki jest zbiór wartości funkcji?

c)    Dla jakich argumentów funkcja przyjmuje wartości ijemne?

d)    Jaka jest nąjwiększa, a jaka nąj-mniejsza wartość funkcji?

e)    Jakie mią)sca zerowe ma funkcja?

X	-7	-5	-3	0	2
0(x)	0	-2	0	12	-8

9---

4.    Sprawdź, które z punktów:

B • (1,2), C-(0,1) należą do wykresu funkcji y - At^J?

5.    a) Znąjdź punkty, w których wykres funkcji y - -$x-4$ przecina osie układu współrzędnych.

b) Zapisz wzór funkcji liniowej, którą) wykres przechodzi przez punkty (2,3) i (-1,8).

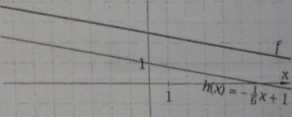
6.    Wykres funkcji f Jest równoległy do wykresu funkcji h. Podaj wzór funkcji f i oblicz ją) miejsca zerowe.

y i

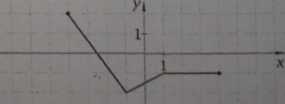
7. Na rysunku przedstawiono wykres funkcji f. Narysuj wykresy funkcji:

a) y = f (x) + 3    c) y-f(x-2)-l

b) y = f(x + 1)    d) y « f[x + 3) + 2

b) y- V5x +1

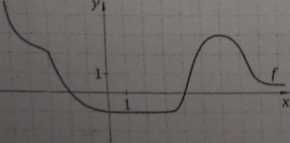
2. Określ przedziały monotonicznośd funkcji przedstawionej na wykresie.

3. Określ dziedzinę funkcji: a)y-^

8. W jaki sposób należy przesunąć wykres funkcji f_% aby otrzymać wykres funkcji 0?

a)    f(x) - | 0(x) - | - 7

b)    f(x) - >/5x g(x) - >/5(x 12)

0 f(x) - g{x) - ^    11