egzam

Wydział Informatyki WIT

l y./iimm / iimtcmulsld dyskretnej (U)

.\'azwisko i Imię

Grupo

UWAGA! W trakcie rozwiązywania zadań należy krótko objaenlać po*tępow.vno powołując n* twlofd/enia litt> /agailmenia kombinatoryczne, z których się korzysta

Wyniki obliczeh stanowląco rozwiązania zadań należy wyróżniać popr/od/ając |# skrótom ..Odp

Nie mogą ono zawierać symboli potęgi ubywającej i przyrastającej, silni oraz współczynnika dwumianowego i wiolomiai^owego. mogą być przedstawione w postaci wyrażeń arytmetycznych zawierających symbole ofMrar.jl dodawania, odejmrmrania. mnożenia l dzielenia oraz zwykłego potęgowania

Potrzebne wartości liczbowe P(n.

‘"I;}

nałoży wy/nnc/Jić rokuroncyjnlo.

Lp.

Madame

Mat.* pki

• Ile jest nicujcmnych i całkowitych rozwiazaó nierówności v, • ,v_: • t, • \.i • .v, • które spełniają warunki: x\.x* c {2.3.4} i .v, ♦ x₇ * vj + .i>, 6 .

2.

lic różnych ciągów symboli zawierających 6 liter i 5 mepowlar/ających się cyfr można utworzy* wybierając litery ze zbioni }3. b. c. d. o. f. g. li. i. k} oraz. cyfry ze /błoni [ I. 2. 3. 4. 5. 6. 7}7

5

5

Na ile sposobów można rozdzielić 13 jednakowych procesów¹ pomiędzy 5 jednakowych procesorów tak. aby na jednym z nich zostały wykonane dokładnie 3 procesy','

Rozdzielić trzeba wszystkie procesy, żaden z. procesorów- nie może pozostać bezczynny i każdy proces musi być w całości wykonany na jednym procesorze

4.

Mamy do dyspozycji 8 osób. wśród których sa dw ie grupy narodowościowe: dwoje bstortezyków i czworo Gruzinów. Na ile sposobów można ustawić te 8 osób w szereg tak. żeby osoby żadnej / tych dwóch narodowości nic stały w komplecie obok siebie?

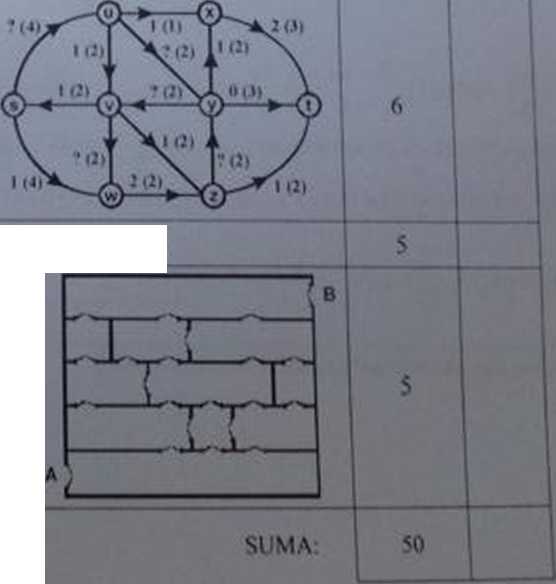
5 Ile jest na podanej kracie ulic najkrótszych dróg z A do B. które przechodzą przynajmniej przez jedno / zaznaczonych skrzyżowań C. D lub E?

I

6.

W pewnym grafie o 16 wierzchołkach maksymalna moc wewnętrznie stabilnego zbioru wierzchołków wynosi 9. Ile wy nosi minimalna moc pokrycia wierzchołkowego w tym grafie?

Czy może w mm istnieć skojarzenie o mocy 8? Odpowiedzi dokładnie uzasadniaj.    _

Podróżnik odwiedził pewien daleki kraj i zapisał w swojej relacji z podróży: „W tym pięknym kraju jest 9 dużych miast Wiele z nich połączonych jest ze sobą utwardzonymi traktami, które nigdzie poza miastami się nic krzyżują. W każdym mieście początek traktu wskazuje specjalna brama / nazwą miasta. do którego on prowadzi. Slolicn ma 7 takich bram. Pięć większych miust mu po 5 takich bram a w każdym z pozostałych są -I takie bramy." Zweryfikuj w oparciu o teorię grafów wiarygodność tej relacji.    _ _

W podanej sieci (przy lukach podano wartości przepływów i w nawiasach ich przepustowości) wyznacz:

a) brakujące wartości przepływów przez luki (ozn ?.i tak. że zostanie zdefiniowany przepływ przez tę sieć; wartość maksymalnego przepływu z. s do t za pomocą kolejnych ścieżek powiększających przepływ; minimalny przekrój pomiędzy s 11 oraz jego przepustowość (zilustruj tw. Forda i Fulkcrsonni

b)

c)

9.

Nary suj wszystkie nicizontorficzne ze sobą graty o 5 wierzchołkach i 4 krawędziach

10. Rozstrzygnij / uzasadnieniem w oparciu o teorię grafów, czy można zwiedzić piętro budynku o podanym obok planie tak. aby wejść drzwiami A. wyjść drzwiami B i przez każde z zaznaczonych drzwi przejść dokładnie raz.

Narjwuj graf reprezentujący zadanie I opis: rozwiązywane zagadnienie w języku teorii grafów.