Elektronikawzad19

W. CmyteU T ELEKTRONIKA W ZADANIACH

Cręłć l- Obliczanie punktów pracy przyu^ilów półpizcwodiuiowych

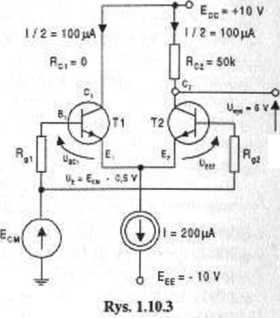
Ponieważ suma prądów la +In musi być stała i równa / (wymusza to idealna - jak zakładamy - siła prądomotoryczna w obwodzie emiterów), towarzyszy temu takie samo zmniejszenie się prądu In (i odpowiedni wzrost napięcia U_Cf₂)- Gdy przy odpowiednio dużym dodatnim napięciu E_x, tranzystor Tl przejmie cały prąd źródła /, tranzystor T2 wchodzi w stan odcięcia, Izn. /a = 0 a Uce2= 10,5 V (zanika spadek napięcia !q-Rc2 i potencjał kolektora Ua = Ecc= 10 V). Spadek napięcia I_c, ■ Ra jest wtedy największy, a zatem napięcie Ucei ma wartość najmniejszą, co z kolei oznacza, że tranzystor Tl mógłby wtedy znajdować się na granicy stanu nasycenia. Jeśli za granicę stanu nasycenia przyjmiemy sytuację gdy U ca = 0 V. odpowiada to potencjałowi kolektora Uc = 0 V (tzn. napięciu Uce= 0,5 V). Tak więc zmianie prądu kolektora w zakresie od zera do pełnego prądu źródła odpowiada zmiana potencjału kolektora od 10 V do zera. Stąd wynika, że maksymalna wartość rezystancji w obwodach kolektorów Ra = Rn = 10 V /200^A = 50 kQ. Przy takiej wartości obydwu rezystorów' Rę w stanie równowagi (£*/ = E_k2 = 0), gdy przez każdy z tranzystorów płynie prąd la = /cz = V4 / = 100 pA potencjały kolektorów są równe i wynoszą Ua = Ua = 5 V i mogą się zmieniać bez zniekształceń w zakresie od zera (granica stanu nasycenia tranzystora) do 10 V (dla stanu odcięcia tranzystora).

Jeśli sygnałem wyjściowym jest napięcie symetryczne pomiędzy kolektorami tranzystorów UvfY sru to stanowi równowagi odpowiada zerowa wartość napięcia wyjściowego (napięcia na obydwu kolektorach są jednakowe), a maksymalna niezniekształcona amplituda wynosi 10 V (od położenia równowagi potencjały obydwu kolektorów mogą się odchylić po 5 V w każdą stronę, przy czym tranzystory pozostają jeszcze w stanie aktywnym). Najczęściej jednak mamy do czynienia z wyjściem niesymetrycznym (tzn. pomiędzy jednym z kolektorów', a masą układu) i wtedy sygnał wyjściowy jest nałożony na składową stałą 5 V, a maksymalna niezniekształcona amplituda składowej zmiennej wynosi 5 V. Rozpatrywany układ ma zastosowanie jako stopień wejściowy wzmacniacza operacyjnego, tzn. wzmacniacza prądu stałego z symetrycznym (różnicowym) wejściem i niesymetrycznym wyjściem. W takim przypadku dążąc do uzyskania zerowego napięcia wyjściowego w stanie rów nowagi musimy jako kolejny stopień wzmocnienia zastosować tzw. układ przesuwania poziomu, który likwiduje opisywane niepożądane przesunięcie napięcia wyjściowego.

W przypadku jak na rysunku, gdy niesymetrycznym napięciem wyjściowym jest napięcie na kolektorze tranzystora T2 czyli U wy = Un, dla rezystora Rei można przyjąć wartość dowolną w zakresie od zera do 50 kii (nie zmienia to rozpływu prądu źródła pomiędzy obydwa tranzystory, a potencjał Ua jest tylko sygnałem wewnętrznym układu).

Przyjęcie wartości Ra mniejszej od 50 kii powoduje, że potencjał Un w stanie równowagi rośnie, a zatem mniejsza może być amplituda górnych połówek składowej zmiennej sygnału wyjściowego. Przyjęcie wartości Rc2 większej od 50 kft powoduje, że potencjał Un w stanic równowagi maleje, a zatem mniejsza może być amplituda dolnych połówek składowej zmiennej sygnału wyjściowego.

Ad 2. Wzrostowi napięcia wejściowego E_si odpowiada wzrost prądu la, zmniejszenie prądu In, a zatem wzrost napięcia wyjściowego Un- Wejście 1 jest zatem wejściem nic odwracającym fezy (przy sygnałach okresowych składowa zmienna napięcia wyjściowego odtwarza kształt napięcia wejściowego, czyli jest z nim zgodna w fazie). Wzrostowi napięcia wejściowego odpowiada wzrost prądu la- czyli opadanie napięcia wyjściowego. Wejście 2 jest zatem wejściem odwracającym fazę (przy symetrycznych sygnałach okresowych składowa zmienna napięcia wyjściowego jest w stosunku do napięcia wejściowego przesunięta w fazie o pół okresu, czyli o 180°). Przy założeniu idealnej symetrii układu wzmocnienia dla obydwu wejść mają taką samą wartość bezwzględną (różnią się tylko znakiem).

O—►

A jak zachowa się układ, gdy (jak na rysunku 1.10.3) na połączone ze sobą wejścia podamy napięcie wspólne £cw? Odpowiada to sytuacji, gdy Egt = Eg2, czyli w idealnie symetrycznym układzie wpływy obydwu wejść wzajemnie się równoważą, tj. napięcie wyjściowe nie ulega zmianie (mówimy, że wzmocnienie dla napięcia wspólnego jest równe zeru). Można to wytłumaczyć także w ten sposób, że napięcie wspólne Ecu nie zmienia rozpływu prądu I pomiędzy dwa identyczne tranzystor)' Tl i T2, a zatem nie wpływa na wartość Uwy- Jedynym skutkiem przyłożenia napięcia wspólnego Ecu jest zmiana potencjału połączonych ze sobą emiterów tranzystorów Tl i T2, a przez to zmiana maksymalnej amplitudy niezniekształconego napięcia wyjściowego. Jeżeli np. Ecm = 2 V to tranzystor T2 wchodzi w stan nasycenia przy U wy = 2 V, a wńęc dla Rc2 = 50 kfl i spoczynkowej wartości U wy = 5 V oznacza to, że ujemna amplituda składowej zmiennej Uwy (pochodzącej od napięcia różnicowego) uległaby zmniejszeniu do 3 V.

W rozpatrywanym układzie dodatnie napięcie wspólne nic może oczywiście przekroczyć wartości + 5 V. kiedy to ujemna amplituda składowej zmiennej Uwy spada do zera. Ujemne napięcie wspólne zwiększa zakres, w którym zmieniają się napięcia Uce czyli pod tym względem na pewno nie pogarsza parametrów wzmacniacza. Zmniejsza ona natomiast różnicę potencjałów, pomiędzy którymi działa SPM wymuszająca prąd /. W rzeczywistym układzie dopuszczalna wartość ujemnego napięcia wspólnego jest uzależniona od własności źródła prądowego /, które w tym zadaniu nie są analizowane.

r U noległe połącz <; jh

SPM o wartości /.- równej prądowi zwarcia dwńjmka.

- ’    • rtpBg rezystąbeji wewnętrznej' dwójnika

widwmej pomiędzy'    żródłaęh.. czy'i prśy

_:    łir^wyciłi;:^pj' działających wewnątrz dwoimfco). \ % ■ 7. |