Elektronikawzad03

W. Ciązyiuki - ELEKTRONIKA W ZADANIACH

Crąić I • OMicnnie punktów pracy przyrządów półprcewinlntiowych

napięcie Us występujące na tym elemencie, jego obrazem graficznym jest tzw. „prosta obciążenia", tj. odcinek linii prostej przecinającej osie układu w punktach A(Ez/ 0) oraz B(0; E_z/ Rz)- Każdemu punktowi na odcinku AB tej prostej odpowiada inna wartość rezystancji obciążającej źródło złożone z siły elektromotorycznej Ez i rezystancji wewnętrznej R_z, przy czym punktowi A odpowiadałoby rozwarcie tych zacisków (prąd w tych warunkach nie płynie, nie ma zatem spadku napięcia na rezystancji wewnętrznej Rz, czyli napięcie na zaciskach zewnętrznych jest równe Ez), a punktowi B odpowiadałoby zwarcie zacisków tego zastępczego źródła (napięcie na tych zaciskach byłoby w tych warunkach równe zeru, a płynący prąd miałby wartość £z//?z).

Jeśli jednak do zacisków źródła zostanie podłączony element nieliniowy o znanej charakterystyce pokazanej przykładowo na rysunku W 1.1, to rozwiązanie tego obwodu stanowią współrzędne punktu P przecięcia tej charakterystyki z prostą obciążenia. Przez element nieliniowy płynie prąd In(P), a na zaciskach zewnętrznych źródła (a zatem także na elemencie nieliniowym) panuje napięcie Us(P).

2. Część liniową zastępujemy silą prądomotoryczną h l rezystancją wewnętrzną Rz* która okazuje się połączona równolegle z elementem nieliniowym (Zasada Nortona, rysunek W 1.2). Dla tego układu na podstawie 1-go prawa KirchhołTa można napisać równanie:

/₂=/,₊/.v    W

a równanie prostej obciążenia - w układzie współrzędnych z rysunku W 1.2, w którym w stosunku do układu z rysunku W1.1 osie /.v i Un zamieniono miejscami - ma postać:

<^wu>

Element nieliniowy, np. dioda

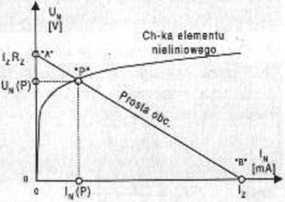
Rys. W1.1 Ilustracja zastosowania zasady Nortona

Także tutaj punktowi A odpowiadałoby rozwarcie zacisków źródła (prąd /a- = 0 i cały prąd l_z płynie przez zastępczą rezystancję wewnętrzną Rz, a napięcie na zaciskach jest równe R_z •b.:)• Punktowi B odpowiadałoby zwarcie zacisków źródła (napięcie na tych zaciskach jest wtedy równe zeru, a zatem prąd 7* = 0 a cały prąd h. płynie przez zwarty obwód zewnętrzny). Współrzędne punktu P przecięcia znanej charakterystyki elementu nieliniowego z opisaną prostą obciążenia stanowią rozwiązanie tego obwodu. Przez element nieliniowy płynie prąd Is(P), a na zaciskach źródła (a zatem także na elemencie nieliniowym) panuje napięcie Un(P)-

Na podstawie powyższych rozważań widzimy więc, że potrafimy rozwiązywać układy prądu stałego z jednym elementem nieliniowym o charakterystyce danej w postaci wykresu (lub równania). Metodę graficzną trudno jednak uznać za wygodną i dlatego w dalszej części zbioru będzie ona wykorzystywana głównie do celów ilustracji uzyskiwanych wyników.

Rozważmy jeszcze krótko możliwości analitycznego rozwiązania obwodu z rysunku Wl.l opisanego równaniem W 1.1. Rozwiązanie jest możliwe, jeśli charakterystykę prądowo-napięciową 7,v = l'(Un) można aproksymować wielomianem, przy czym trudności rosną gwałtownie ze wzrostem stopnia tego wielomianu. Gdybyśmy jednak np. dla diody półprzewodnikowej chcieli wykorzystać znaną zależność wykładniczą prądu lp od napięcia Vp:

/,,=/Jexp(^£-)-l)    (Wl.S)

gdzie:

/_v = prąd nośników mniejszościowych płynący przez złącze spolaryzowane zaporowo;

q= ładunek elektronu; k - stała Boltzmanna;

T = temperatura bezwzględna [Kj;

to przyjmując I_D = I_N oraz U_D= Us otrzymujemy równanie przestępne:

E₇, =U„    ■/„ ={/„+*, •/, [exp4^-)-H    (WJ.6)

k-T

możliwe do rozwiązania tylko numerycznie. Tak więc ta droga postępowania jest dla naszych celów całkowicie nieprzydatna.

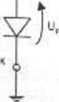
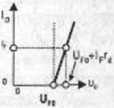
W większości przypadków możliwe jest jednak łatwe uzyskanie rozwiązania na drodze analitycznej, jeśli zgodzimy się na pewne pogorszenie jego dokładności wynikające z przyjęcia dodatkowych uproszczeń. Na przykład nieliniową charakterystykę diody półprzewodnikowej (lub złącza baza-emiter tranzystora bipolarnego) możemy dla kierunku przewodzenia zastąpić siłą elektromotoryczną Uf równą przybliżonemu spadkowi napięcia na diodzie, lub szeregowym połączeniem takiej SEM i rezystancji dynamicznej rj diody w oczekiwanym zakresie prądów (Rysunek W1.3).

1		*JL «F= <u2as-uf)/r Oy* UFnie zal. od 1F		,
	R
		X		^0

^A    lub

'_F«dW u_ro)/( H + g

U_F=U_F0^+Ir^rd

Ik

Rys. W 1.3. Schematy zastępcze diody spolaryzowanej w kierunku przewodzenia